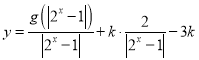题目内容
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)函数![]() 若存在
若存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数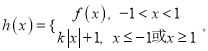 讨论函数
讨论函数![]() 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程).
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】【试题分析】(1)先判断出函数![]() 的是定义在区间
的是定义在区间![]() 上的减函数,然后将所求不等式等价转化为
上的减函数,然后将所求不等式等价转化为![]() 即
即![]() ,由此求得解集为
,由此求得解集为![]() .(2)由题意知:
.(2)由题意知: ![]() 时,
时, ![]() 值域有交集.
值域有交集. ![]() 时,
时, ![]() 是减函数
是减函数![]() 对
对![]() 分成两类讨论得出
分成两类讨论得出![]() 的值域,由此求得
的值域,由此求得![]() 的取值范围.(3)由
的取值范围.(3)由![]() ,得
,得![]() ,令
,令![]() 则
则![]() 作出图像,对
作出图像,对![]() 分类,结合图象讨论零点的个数.
分类,结合图象讨论零点的个数.
【试题解析】
(1)![]() ,定义域为
,定义域为![]()
![]() ,函数
,函数![]() 是奇函数.
是奇函数.
又![]() 在
在![]() 时是减函数,(也可用定义法证明)
时是减函数,(也可用定义法证明)
故不等式![]() 等价于
等价于![]()
即![]() ,
,
![]() 又
又![]()
故不等式![]() 的解集为
的解集为![]() .
.
(2)由题意知: ![]() 时,
时, ![]() 值域有交集.
值域有交集.
![]() 时,
时, ![]() 是减函数
是减函数![]()
当![]() 时,
时, ![]() 时单调递减,
时单调递减, ![]()
![]()
![]()
当![]() 时,
时, ![]() 时单调递增,
时单调递增, ![]() 显然不符合
显然不符合
综上: ![]() 的取值范围为
的取值范围为![]()
(3)由![]() ,得
,得![]() ,令
,令![]() 则
则![]()
作出图像

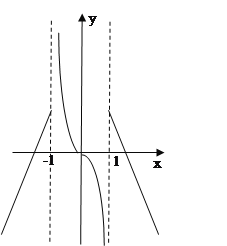
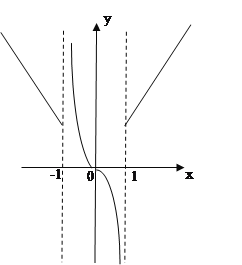
由图可知,①当![]() 时,由
时,由![]() 得出
得出![]() ,
,
当![]() 时,
时, ![]() ,对应有3个零点;
,对应有3个零点;
当![]() 时,
时, ![]() ,对应有1个零点;
,对应有1个零点;
②当![]() 时,只有一个
时,只有一个![]() ,对应有1个零点;
,对应有1个零点;
③当![]() 时,只有一个
时,只有一个![]() ,对应只有一个零点;
,对应只有一个零点;
④当![]() 时,
时, ![]() ,此时
,此时![]()
![]() ,
, ![]() ,
,
由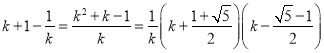
得在![]() 时,
时, ![]() ,三个
,三个![]() 分别对应一个零点,共3个,
分别对应一个零点,共3个,
在![]() 时,
时, ![]() ,三个
,三个![]() 分别对应1个,1个,3个零点,共5个.
分别对应1个,1个,3个零点,共5个.
综上所述,当![]() 或
或![]() 或
或![]() 时,函数
时,函数![]() 只有1个零点;
只有1个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有3个零点;
有3个零点;
当![]() 时,函数
时,函数![]() 有5个零点.
有5个零点.

练习册系列答案
相关题目