题目内容
(本小题满分14分)已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量m=(sinA,1), n=(1,-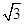 cosA),且m⊥n.
cosA),且m⊥n.
(1)求角A; (2)若b+c=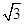 a,求sin(B+
a,求sin(B+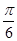 )的值.
)的值.
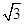 cosA),且m⊥n.
cosA),且m⊥n.(1)求角A; (2)若b+c=
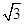 a,求sin(B+
a,求sin(B+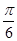 )的值.
)的值.解:(1)因为m⊥n,所以m·n=0,即sinA-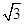 cosA=0.所以sinA=
cosA=0.所以sinA=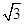 cosA,得tanA=
cosA,得tanA=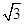 .又因为0<A<π,所以A=
.又因为0<A<π,所以A=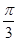 .
.
(2)(法1)因为b+c=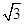 a,由正弦定理得sinB+sinC=
a,由正弦定理得sinB+sinC=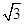 sinA=
sinA=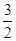 .
.
因为B+C=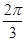 ,所以sinB+sin(
,所以sinB+sin(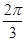 -B)=
-B)=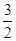 .化简得
.化简得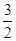 sinB+
sinB+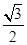 cosB=
cosB=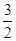 ,
,
从而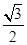 sinB+
sinB+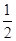 cosB=
cosB=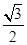 ,即sin(B+
,即sin(B+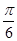 )=
)=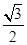 .
.
(法2)由余弦定理可得b2+c2-a2=2bccosA,即b2+c2-a2=bc ①.又因为b+c=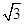 a ②,
a ②,
联立①②,消去a得2b2-5bc+2c2=0,即b=2c或c=2b.若b=2c,则a=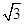 c,可得B=
c,可得B=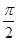 ;若c=2b,则a=
;若c=2b,则a=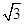 b,可得B=
b,可得B=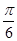 .所以sin(B+
.所以sin(B+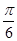 )=
)=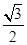 .
.
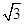 cosA=0.所以sinA=
cosA=0.所以sinA=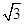 cosA,得tanA=
cosA,得tanA=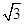 .又因为0<A<π,所以A=
.又因为0<A<π,所以A=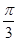 .
.(2)(法1)因为b+c=
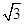 a,由正弦定理得sinB+sinC=
a,由正弦定理得sinB+sinC=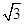 sinA=
sinA=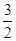 .
.因为B+C=
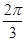 ,所以sinB+sin(
,所以sinB+sin(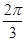 -B)=
-B)=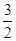 .化简得
.化简得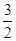 sinB+
sinB+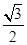 cosB=
cosB=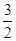 ,
,从而
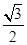 sinB+
sinB+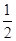 cosB=
cosB=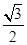 ,即sin(B+
,即sin(B+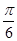 )=
)=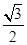 .
.(法2)由余弦定理可得b2+c2-a2=2bccosA,即b2+c2-a2=bc ①.又因为b+c=
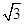 a ②,
a ②,联立①②,消去a得2b2-5bc+2c2=0,即b=2c或c=2b.若b=2c,则a=
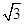 c,可得B=
c,可得B=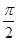 ;若c=2b,则a=
;若c=2b,则a=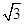 b,可得B=
b,可得B=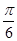 .所以sin(B+
.所以sin(B+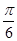 )=
)=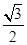 .
.略

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
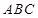 中,角
中,角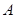 、
、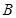 、
、 的对边分别为
的对边分别为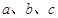 ,满足
,满足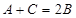 ,且
,且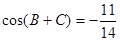 .
.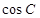 的值;
的值; 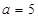 ,求△
,求△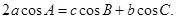
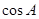 的值;
的值;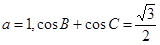 ,求边c的值.
,求边c的值.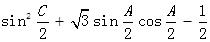 的取值范围.
的取值范围.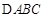 中,
中, 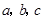 分别为角
分别为角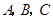 的对边,且满足
的对边,且满足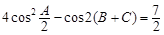 .
.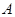 大小;(2)若
大小;(2)若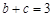 ,求
,求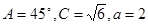 的△ABC的个数为m,则am的值为 ( )
的△ABC的个数为m,则am的值为 ( )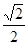 ,AC=2,AB=3,
,AC=2,AB=3,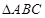 中,已知BC=1,B=
中,已知BC=1,B=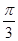 ,则
,则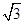 ,则AC和长为 ▲
,则AC和长为 ▲ 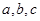 ,向量
,向量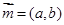 ,
,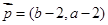 ,若
,若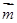 ⊥
⊥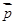 ,边长
,边长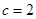 ,角C =
,角C =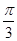 ,则ΔABC的面积是
,则ΔABC的面积是