题目内容
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: ![]() 表示一辆车从甲地到乙地遇到红灯的个数,
表示一辆车从甲地到乙地遇到红灯的个数, ![]() 的所有可能取值为0,1,2,3.分别求出相应的概率值,列出随机变量
的所有可能取值为0,1,2,3.分别求出相应的概率值,列出随机变量![]() 的分布列并计算数学期望,
的分布列并计算数学期望, ![]() 表示第一辆车遇到红灯的个数,
表示第一辆车遇到红灯的个数, ![]() 表示第二辆车遇到红灯的个数,这2辆车共遇到1个红灯就是包括第一辆遇到1次红灯且第2辆没遇上和第一辆没遇上红灯且第2辆遇上1次红灯两个事件的概率的和.
表示第二辆车遇到红灯的个数,这2辆车共遇到1个红灯就是包括第一辆遇到1次红灯且第2辆没遇上和第一辆没遇上红灯且第2辆遇上1次红灯两个事件的概率的和.
试题解析:(Ⅰ)解:随机变量![]() 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
随机变量![]() 的数学期望
的数学期望![]() .
.
(Ⅱ)解:设![]() 表示第一辆车遇到红灯的个数,
表示第一辆车遇到红灯的个数, ![]() 表示第二辆车遇到红灯的个数,则所求事件的概率为
表示第二辆车遇到红灯的个数,则所求事件的概率为![]()
![]() .
.
所以,这2辆车共遇到1个红灯的概率为![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
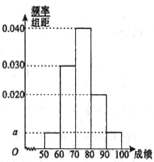
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(Ⅲ)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
(参考公式:![]() ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |