题目内容
(本小题满分12分)
椭圆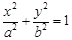
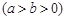 过点
过点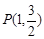 ,其左、右焦点分别为
,其左、右焦点分别为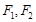 ,离心率
,离心率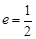 ,
,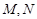 是直线
是直线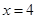 上的两个动点,且
上的两个动点,且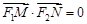 .
.
(1)求椭圆的方程; (2)求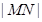 的最小值;
的最小值;
(3)以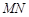 为直径的圆
为直径的圆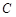 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
椭圆
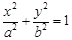
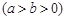 过点
过点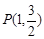 ,其左、右焦点分别为
,其左、右焦点分别为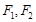 ,离心率
,离心率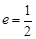 ,
,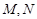 是直线
是直线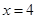 上的两个动点,且
上的两个动点,且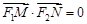 .
.(1)求椭圆的方程; (2)求
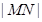 的最小值;
的最小值;(3)以
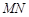 为直径的圆
为直径的圆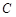 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.解:(1)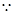
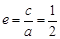 ,且过点
,且过点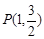 ,
,
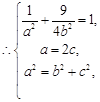 解得
解得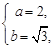
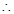 椭圆方程为
椭圆方程为  .…………4分
.…………4分
 设点
设点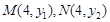 则
则
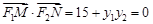 ,
,
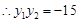 , 又
, 又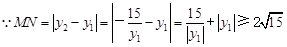 ,
,
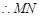 的最小值为
的最小值为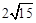 .……………………… 7分
.……………………… 7分
 圆心
圆心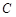 的坐标为
的坐标为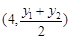 ,半径
,半径 .
.
圆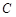 的方程为
的方程为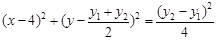 ,
,
整理得: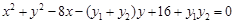 . …………10分
. …………10分
 ,
,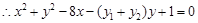 令
令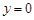 ,得
,得 ,
,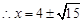 .
.
圆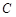 过定点
过定点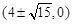 .………………12分
.………………12分
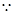
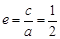 ,且过点
,且过点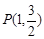 ,
,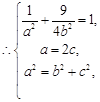 解得
解得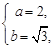
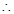 椭圆方程为
椭圆方程为  .…………4分
.…………4分 设点
设点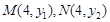 则
则
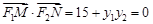 ,
,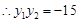 , 又
, 又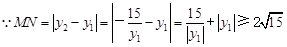 ,
,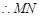 的最小值为
的最小值为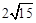 .……………………… 7分
.……………………… 7分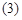 圆心
圆心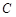 的坐标为
的坐标为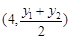 ,半径
,半径 .
.圆
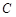 的方程为
的方程为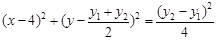 ,
, 整理得:
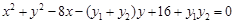 . …………10分
. …………10分 ,
,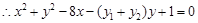 令
令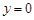 ,得
,得 ,
,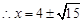 .
. 圆
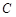 过定点
过定点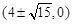 .………………12分
.………………12分略

练习册系列答案
相关题目
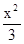 +
+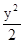 =1与椭圆
=1与椭圆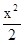 +
+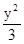 =l(l>0)有 ( )
=l(l>0)有 ( )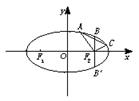
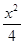 +
+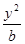 =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于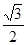 ,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上.
,抛物线C2:x2=2py(p>0)的焦点在椭圆C1的顶点上. 的左焦点
的左焦点 是长轴的一个四等分点,点A、B分别为椭圆的左、右顶点,过点F且不与y轴垂直的直线
是长轴的一个四等分点,点A、B分别为椭圆的左、右顶点,过点F且不与y轴垂直的直线 交椭圆于C、D两点,记直线AD、BC的斜率分别为
交椭圆于C、D两点,记直线AD、BC的斜率分别为
 轴时,求
轴时,求 的值;
的值;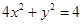 上,则
上,则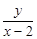 的最小值为( )
的最小值为( )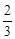

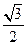 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标.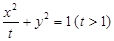 上一焦点与短轴两端点形成的三角形的面积为1,则
上一焦点与短轴两端点形成的三角形的面积为1,则 .
.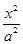 +
+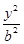 =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若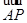 =2
=2 ,则椭圆的离心率是( )
,则椭圆的离心率是( )


