题目内容
已知椭圆x2+(m+3)y2=m(m>0)的离心率e=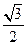 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标.
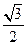 ,求m的值及椭圆的长轴和短轴的长及顶点坐标.
,求m的值及椭圆的长轴和短轴的长及顶点坐标.解:椭圆方程可化为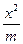 +
+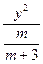 =1.
=1.
因为m-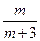 >0,所以m>
>0,所以m>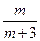 .
.
即a2=m,b2=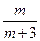 ,c=
,c=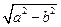 .
.
由e=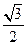 ,解得m=1.
,解得m=1.
所以a=1,b=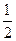 ,椭圆的标准方程为x2+
,椭圆的标准方程为x2+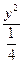 =1.
=1.
所以椭圆的长轴长为2,短轴长为1,
四个顶点的坐标分别为
A1(-1,0),A2(1,0),B1(0,-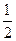 ),B2(0,
),B2(0,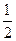 )
)
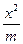 +
+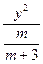 =1.
=1.因为m-
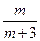 >0,所以m>
>0,所以m>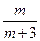 .
.即a2=m,b2=
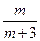 ,c=
,c=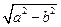 .
.由e=
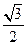 ,解得m=1.
,解得m=1.所以a=1,b=
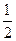 ,椭圆的标准方程为x2+
,椭圆的标准方程为x2+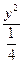 =1.
=1.所以椭圆的长轴长为2,短轴长为1,
四个顶点的坐标分别为
A1(-1,0),A2(1,0),B1(0,-
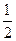 ),B2(0,
),B2(0,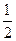 )
)略

练习册系列答案
相关题目
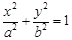
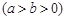 过点
过点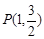 ,其左、右焦点分别为
,其左、右焦点分别为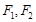 ,离心率
,离心率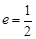 ,
,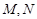 是直线
是直线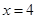 上的两个动点,且
上的两个动点,且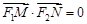 .
.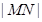 的最小值;
的最小值;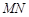 为直径的圆
为直径的圆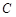 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.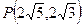 ,且与椭圆
,且与椭圆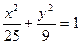 有相同焦点的椭圆的标准方程.
有相同焦点的椭圆的标准方程.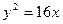 的焦点
的焦点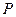 为其一个焦点,以双曲线
为其一个焦点,以双曲线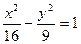 的焦点
的焦点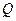 为顶点。
为顶点。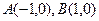 ,且
,且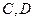 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点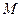 是线段
是线段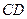 上的动点,求
上的动点,求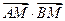 的取值范围。
的取值范围。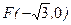 ,且过
,且过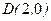 ,设点
,设点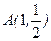 .
.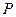 是椭圆上的动点,求线段
是椭圆上的动点,求线段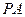 中点
中点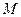 的轨迹方程;
的轨迹方程;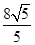 B
B 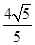 C
C 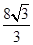 D
D 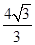
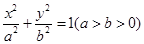 的左准线上,过点P斜率为
的左准线上,过点P斜率为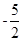 的光线,
的光线,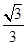
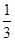
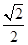
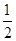
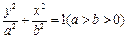 的右顶点与上顶点分别
的右顶点与上顶点分别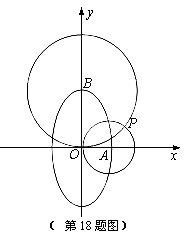
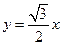 上,求椭圆的离心率;
上,求椭圆的离心率;



