题目内容
8.在△ABC中,角A,B,C的对边分别为a,b,c,且bcosC=(3a-c)cosB.(Ⅰ)求cosB的值.
(Ⅱ)若$b=\sqrt{3}$,且a=c,求△ABC的面积.
分析 (Ⅰ)在△ABC中,由条件利用正弦定理可得sinBcosC=3sinAcosB-sinCcosB,即sin(B+C)=3sinAcosB,由此求得cosB的值.
(Ⅱ)由条件利用余弦定理求得a=c的值,再根据△ABC的面积为 $\frac{1}{2}$ac•sinB,计算求的结果.
解答 解:(Ⅰ)在△ABC中,∵bcosC=(3a-c)cosB,利用正弦定理可得sinBcosC=3sinAcosB-sinCcosB,
∴sin(B+C)=sinA=3sinAcosB,∴cosB=$\frac{1}{3}$.
(Ⅱ)若$b=\sqrt{3}$,且a=c,则由余弦定理可得 b2=3=a2+a2-2a•a•cosB,求得a=c=$\frac{3}{2}$,
∴△ABC的面积为 $\frac{1}{2}$ac•sinB=$\frac{1}{2}$×$\frac{9}{4}$×$\frac{2\sqrt{2}}{3}$=$\frac{3\sqrt{2}}{4}$.
点评 本题主要考查正弦定理和余弦定理的应用,诱导公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某地四月份刮东风的概率是$\frac{8}{30}$,既刮东风又下雨的概率是$\frac{7}{30}$,则该地四月份刮东风的条件下,下雨的概率为( )
| A. | $\frac{8}{30}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{30}$ |
3.下列命题中,真命题是( )
| A. | ?x0∈[0,$\frac{π}{2}$],sin x0+cos x0≥2 | B. | ?x∈(3,+∞),x2>2x+1 | ||
| C. | ?x0∈R,x02+x0=-1 | D. | ?x∈($\frac{π}{2}$,π),tan x>sin x |
13.集合A={(x,y)|y=lg(x+1)-1},B={(x,y)|x=m},若A∩B=∅,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-1) | D. | (-∞,-1] |
20.在25件同类产品中,有2件次品,从中任取3件产品,其中不可能事件为( )
| A. | 3件都是正品 | B. | 至少有1次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
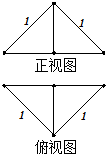 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.