题目内容
4.若函数f(x)=$\frac{bx+2}{x+a}$为奇函数,则a=0,b=0.分析 根据函数奇偶性的定义和性质进行求解即可.
解答 解:∵函数f(x)=$\frac{bx+2}{x+a}$为奇函数,
∴f(-x)=-f(x),
即$\frac{-bx+2}{-x+a}$=-$\frac{bx+2}{x+a}$,
即(x+a)(2-bx)=(bx+2)(x-a),
即-bx2+(2-ab)x+2a=bx2+(2-ab)x-2a,
则-b=b且2a=-2a,
解得a=0,b=0,
故答案为:0,0
点评 本题主要考查函数奇偶性的应用,根据条件f(-x)=-f(x),进行对比即可.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
15.如图所示的是一个几何体的三视图,则它的表面积为( )
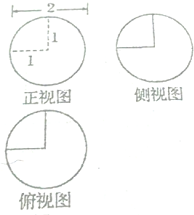

| A. | 4π | B. | $\frac{15π}{4}$ | C. | 5π | D. | $\frac{17π}{4}$ |
12.一质点由A点出发沿直线AB运动,先以加速度大小为a1的匀加速运动,接着做加速度为a2的匀减速直线运动,抵达B点时恰好静止,如果AB的总长度为S,试求质点走完AB全程所用时间t.(用多种方法求解)
9.已知集合A={y|y=-x2+5x-4,x∈R},则有( )
| A. | 1∈A且4∈A | B. | 1∈A但4∉A | C. | 1∉A但4∈A | D. | 1∉A且4∉A |