题目内容
【题目】已知半径为 ![]() ,圆心在直线l1:x﹣y+1=0上的圆C与直线l2:
,圆心在直线l1:x﹣y+1=0上的圆C与直线l2: ![]() x﹣y+1﹣
x﹣y+1﹣ ![]() =0相交于M,N两点,且|MN|=
=0相交于M,N两点,且|MN|= ![]()
(1)求圆C的标准方程;
(2)当圆心C的横、纵坐标均为整数时,若对任意m∈R,直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,求实数a的取值范围.
+1=0与圆C恒有公共点,求实数a的取值范围.
【答案】
(1)解:由题意,设C(a,a+1),圆心到直线的距离d= 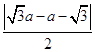 =
= ![]() ,
,
∴a=0或3+ ![]() ,
,
∴圆C的标准方程为x2+(y﹣1)2=5或(x﹣3﹣ ![]() )2+(y﹣4﹣
)2+(y﹣4﹣ ![]() )2=5;
)2=5;
(2)解:圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,
直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,
+1=0与圆C恒有公共点,
∴ 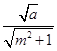 ≤
≤ ![]() ,
,
∴0≤a≤5(m2+1),∴0≤a≤5.
【解析】(1)由题意,设C(a,a+1),圆心到直线的距离d= ![]() =
= ![]() ,求出a,可得圆C的标准方程;(2)圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,直线l3:mx﹣y+
,求出a,可得圆C的标准方程;(2)圆C的标准方程为x2+(y﹣1)2=5,对任意m∈R,直线l3:mx﹣y+ ![]() +1=0与圆C恒有公共点,
+1=0与圆C恒有公共点, ![]() ≤
≤ ![]() ,即可求实数a的取值范围.
,即可求实数a的取值范围.
【考点精析】掌握直线与圆的三种位置关系是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】某研究机构对中学生记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x | 4 | 6 | 8 | 10 |
识图能力y | 3 | ﹡﹡﹡ | 6 | 8 |
由于某些原因,识图能力的一个数据丢失,但已知识图能力样本平均值是5.5.
(Ⅰ)求丢失的数据;
(Ⅱ)经过分析,知道记忆能力x和识图能力y之间具有线性相关关系,请用最小二乘法求出y关于x的线性回归方程 ![]() ;
;
(III)若某一学生记忆能力值为12,请你预测他的识图能力值.