题目内容
7.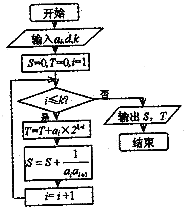 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在最小的正数m,使得?n∈N+,都有T≤m成立?若存在,求出m的值,若不存在,请说明理由.
分析 (1)由图表结合裂项相消法求得Sk,再由已知可得a1a6=-9且a1a11=-99,求出首项和公差后得答案;
(2)由图表可得Tk,然后利用错位相减法求得Tk,得到${T}_{k+1}-{T}_{k}=\frac{9-2k}{{2}^{k}}$,可得:$({T}_{k})_{max}={T}_{5}=\frac{227}{16}$,即m=$\frac{227}{16}$.
解答 解:(1)根据框图:
${S}_{k}=\frac{1}{{a}_{1}{a}_{2}}+\frac{1}{{a}_{2}{a}_{3}}+…+\frac{1}{{a}_{k}{a}_{k+1}}$=$\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{2}}+\frac{1}{{a}_{2}}-\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{k}}-\frac{1}{{a}_{k+1}})$=$\frac{k}{{a}_{1}{a}_{k+1}}$.
∴有a1a6=-9且a1a11=-99,
解得a1=9,d=-2,
∴an=11-2n.
(2)事实上,${T_k}={a_1}•{2^0}+{a_2}•{2^{-1}}+{a_3}•{a^{-2}}+…+{a_k}•{2^{1-k}}$,
$\frac{1}{2}{T}_{k}={a}_{1}•{2}^{-1}+{a}_{2}•{2}^{-2}+…+{a}_{k}•{2}^{-k}$,
两式作差得:$\frac{1}{2}{T}_{k}={a}_{1}+d({2}^{-1}+{2}^{-2}+…+{2}^{1-k})-{a}_{k}•{2}^{-k}$,
∴${T}_{k}=14+\frac{2k-7}{{2}^{k-1}}$,
从而${T}_{k+1}-{T}_{k}=\frac{9-2k}{{2}^{k}}$,
得:$({T}_{k})_{max}={T}_{5}=\frac{227}{16}$,即m=$\frac{227}{16}$.
点评 本题考查程序框图,考查学生读取图表的能力,训练了裂项相消法和错位相减法求数列的前n项和,属中高档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
| A. | i≤2012 | B. | i>2012 | C. | i≤1006 | D. | i>1006 |
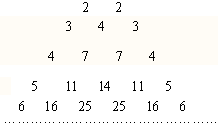 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n, 已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$.
已知an=$\frac{n}{2015}$,把数列{an}中的各项排成如图所示的三角形形状,记A(m,n)表示第m行的第n个数,则A(9,13)表示的数为$\frac{77}{2015}$.