题目内容
18.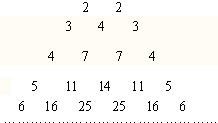 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n,(2)表中每行由n开始逐渐变大,然后变小,回到n,除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第n行第k个数字等于第n-1行的第k-1个数字与第k个数字的和).
那么第19行的第2个数比第18行的第2个数大18;第n行(n≥2)第2个数是$\frac{{n}^{2}-n+2}{2}$.
分析 依据“中间的数从第三行起,每一个数等于它两肩上的数之和”则第二个数等于上一行第一个数与第二个数的和,即有an+1=an+n(n≥2),再由累加法求解.
解答 解:把第n行(n≥2)第2个数记为an,
则由题意可知a2=2,a3=4,a4=7,a5=11,
所以a3-a2=2,a4-a3=3,a5-a4=4…an-an-1=n-1,
以上n-1个等式相加得,an-a2=2+3+…+(n-1)=$\frac{(n-2)(n+1)}{2}$,
所以an=2+$\frac{(n-2)(n+1)}{2}$=$\frac{{n}^{2}-n+2}{2}$(n≥2),
故答案为:18;$\frac{{n}^{2}-n+2}{2}$.
点评 本题通过三角数表构造了一系列数列,考查了数列的通项及求和的方法,还考查了数列间的关系,入题较难,知识点,方法活,属中档题.

练习册系列答案
相关题目
8.若有关x的方程x2lnx=kx-1有实数解,则实数k的取值范围为( )
| A. | (-∞,-1]∪[1,+∞) | B. | (-∞,-1] | C. | [1,+∞) | D. | (-∞,-1]∪(1,+∞) |
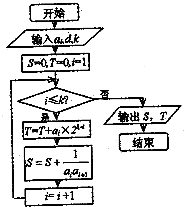 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)