题目内容
2.求函数y=log24x•log22x 在$\frac{1}{4}$≤x≤4的最值,并给出最值时对应的x的值.分析 令t=log2x,确定出t=log2x的最大值和最小值,进而得到t取值范围;由已知中f(x)=log2(4x)•log2(2x),用换元法,将问题转化为一个二次函数在定区间上的最值问题,根据二次函数的性质易得答案.
解答 解:令t=log2x,则
∵$\frac{1}{4}$≤x≤4,
∴log2$\frac{1}{4}$≤t≤log24,即-2≤t≤2
y=(log2x)2+3log2x+2=$(t+\frac{3}{2})^{2}-\frac{1}{4}$,
∴t=-$\frac{3}{2}$,即x=${2}^{-\frac{3}{2}}$,f(x)min=-$\frac{1}{4}$;当t=2即x=4时,f(x)max=12.
点评 本题考查的知识点是对数函数的图象与性质的综合应用,二次函数在定区间上的最值问题,熟练掌握对数函数的性质和二次函数的性质是解答本题的关键.

练习册系列答案
相关题目
12.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(x,-6),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | -$\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | -$\frac{2}{9}$ | D. | $\frac{2}{9}$ |
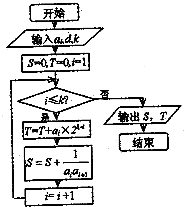 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)