题目内容
17.已知点A(0,1),B(1,0),C(1,2),D(2,1),问$\overrightarrow{AB}$与$\overrightarrow{CD}$是否共线.分析 根据平面向量的坐标运算,求出向量$\overrightarrow{AB}$与$\overrightarrow{CD}$,即可判断它们是否共线.
解答 解:∵A(0,1),B(1,0),C(1,2),D(2,1),
∴$\overrightarrow{AB}$=(1,-1),
$\overrightarrow{CD}$=(1,-1),
∴$\overrightarrow{AB}$=$\overrightarrow{CD}$,
$\overrightarrow{AB}$与$\overrightarrow{CD}$共线.
点评 本题考查了平面向量的坐标运算以及向量的共线定理,是基础题目.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8.若有关x的方程x2lnx=kx-1有实数解,则实数k的取值范围为( )
| A. | (-∞,-1]∪[1,+∞) | B. | (-∞,-1] | C. | [1,+∞) | D. | (-∞,-1]∪(1,+∞) |
12.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(x,-6),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | -$\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | -$\frac{2}{9}$ | D. | $\frac{2}{9}$ |
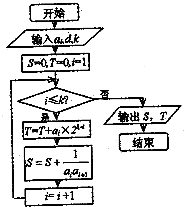 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)