题目内容
17.设Sn为等差数列{an}的前n项和,若a1=$\frac{1}{2}$,S2=a3,则a5=$\frac{5}{2}$.分析 设公差为d,利用a1=$\frac{1}{2}$,S2=a3,可得$\frac{1}{2}+\frac{1}{2}+d=\frac{1}{2}+2d$,求出公差,即可得出结论.
解答 解:设公差为d,则
∵a1=$\frac{1}{2}$,S2=a3,
∴$\frac{1}{2}+\frac{1}{2}+d=\frac{1}{2}+2d$,
∴d=$\frac{1}{2}$,
∴a5=$\frac{1}{2}+4•\frac{1}{2}$=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查等差数列的通项公式的运用,考查学生的计算能力,确定公差是关键.

练习册系列答案
相关题目
2.在(1+x)3+(1+x)4+(1+x)5+(1+x)6+(1+x)7的展开式中,x3的系数为( )
| A. | C${\;}_{7}^{4}$ | B. | C${\;}_{8}^{4}$ | C. | C${\;}_{8}^{3}$ | D. | C${\;}_{9}^{3}$ |
9.设全集为R,集合A={x||x|<3},B={x|-1<x≤5},则A∩(∁RB)=( )
| A. | (-3,0) | B. | (-3,-1] | C. | (-3,-1) | D. | (-3,3) |
7.某商品在5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是$\stackrel{∧}{y}$=-3.2x+4a,则a=10.
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
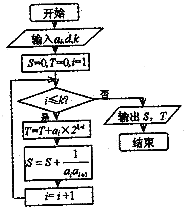 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)