题目内容
设f (x)=|2-x2|,若0<a<b且f (a)="f" (b),则a+b的取值范围是( )
| A.(0,2) | B.( , 2) , 2) | C.(2,4) | D.(2,2 ) ) |
D
解:
当x<0时,f(x)= -x2+2(- 2 <x<0)
x2-2(x≤- 2 )
∴f(x)在(-∞,- 2 )递增;在(- 2 ,0)
∵a<b<0,且f(a)=f(b),
∴-a≤-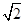 ,b>2-
,b>2-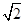 且a2-2="-" a2+2
且a2-2="-" a2+2
解得a=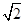 ;2-
;2- 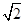 <b<
<b<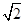
故选D
当x<0时,f(x)= -x2+2(- 2 <x<0)
x2-2(x≤- 2 )
∴f(x)在(-∞,- 2 )递增;在(- 2 ,0)
∵a<b<0,且f(a)=f(b),
∴-a≤-
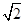 ,b>2-
,b>2-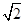 且a2-2="-" a2+2
且a2-2="-" a2+2解得a=
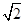 ;2-
;2- 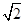 <b<
<b<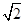
故选D

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
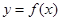 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为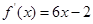 ,数列
,数列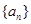 的前n项和为
的前n项和为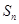 ,点
,点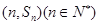 均在函数
均在函数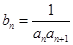 ,
,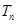 是数列
是数列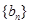 的前n项和,求使得
的前n项和,求使得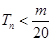 对所有
对所有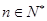 都成立的最小正整数m;
都成立的最小正整数m; 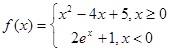 ,若存在不同的实数
,若存在不同的实数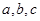 使得
使得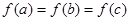 ,则
,则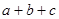 的取值范围是
的取值范围是 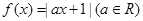 ,不等式
,不等式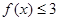 的解集为
的解集为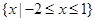
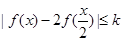 恒成立,求k的取值范围。
恒成立,求k的取值范围。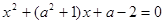 ,有一个根比
,有一个根比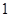 大,另一个根比
大,另一个根比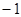 小,则
小,则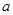 的取值范围是( )
的取值范围是( )

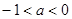

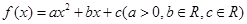 ,若函数
,若函数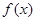 的最小值是
的最小值是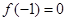 ,
,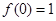 且对称轴是
且对称轴是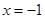
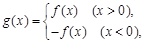 求
求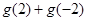 的值;
的值;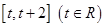 的最小值.
的最小值.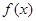 ,若存在
,若存在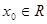 ,使得
,使得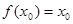 成立,则称
成立,则称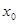 为
为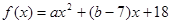 的两个天宫一号点分别是
的两个天宫一号点分别是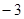 和2 .
和2 .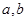 的值及
的值及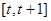 上的最大值
上的最大值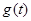 .
.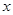 的实系数一元二次方程
的实系数一元二次方程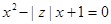
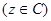 有实数根,则
有实数根,则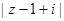 的最小值为___
的最小值为___ 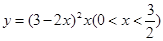 的最大值是 。
的最大值是 。