题目内容
对于函数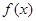 ,若存在
,若存在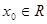 ,使得
,使得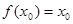 成立,则称
成立,则称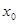 为
为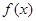 的天宫一号点.已知函数
的天宫一号点.已知函数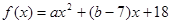 的两个天宫一号点分别是
的两个天宫一号点分别是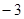 和2 .
和2 .
(1)求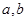 的值及
的值及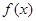 的表达式;
的表达式;
(2)试求函数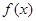 在区间
在区间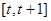 上的最大值
上的最大值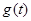 .
.
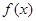 ,若存在
,若存在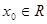 ,使得
,使得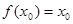 成立,则称
成立,则称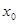 为
为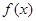 的天宫一号点.已知函数
的天宫一号点.已知函数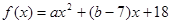 的两个天宫一号点分别是
的两个天宫一号点分别是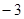 和2 .
和2 .(1)求
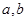 的值及
的值及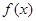 的表达式;
的表达式; (2)试求函数
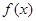 在区间
在区间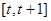 上的最大值
上的最大值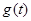 .
.(1)依题意得 ;
;
即 ,…………………………2分
,…………………………2分
解得
 ………………4分
………………4分
(2)
∴函数的最大值求值问题可分成三种情况:
(1)当 时,
时,  上单调递减,
上单调递减,
∴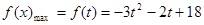 ; …………………………6分
; …………………………6分
(2)当 时, 即
时, 即 ,
,  上单调递增,
上单调递增,
∴ …………………………8分
…………………………8分
(3)当 且
且 时, 即
时, 即 ,
,  上不单调, 此时
上不单调, 此时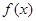 的最大值在抛物线的顶点处取得.
的最大值在抛物线的顶点处取得.
∴ …………………………10分
…………………………10分
故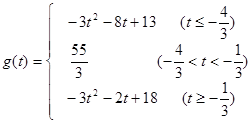
 ;
;即
 ,…………………………2分
,…………………………2分解得

 ………………4分
………………4分(2)

∴函数的最大值求值问题可分成三种情况:
(1)当
 时,
时,  上单调递减,
上单调递减, ∴
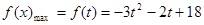 ; …………………………6分
; …………………………6分(2)当
 时, 即
时, 即 ,
,  上单调递增,
上单调递增,∴
 …………………………8分
…………………………8分(3)当
 且
且 时, 即
时, 即 ,
,  上不单调, 此时
上不单调, 此时 的最大值在抛物线的顶点处取得.
的最大值在抛物线的顶点处取得. ∴
 …………………………10分
…………………………10分故
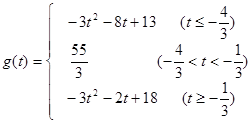
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 , 2)
, 2) ,
, ,则函数
,则函数 的值域为 .
的值域为 . ,若
,若 ,则
,则 =( )
=( )



 ,那么( )
,那么( )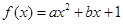 及函数
及函数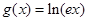 ,函数
,函数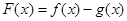 在
在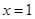 处取得极值.
处取得极值.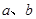 所满足的关系式;
所满足的关系式;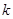 ,使得对(Ⅰ)中任意的实数
,使得对(Ⅰ)中任意的实数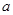 ,直线
,直线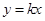 与函数
与函数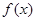 在
在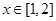 上的图像恒有公共点?若存在,求出
上的图像恒有公共点?若存在,求出
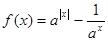 (其中
(其中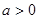 且
且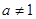 ,
,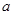 为实常数).
为实常数).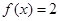 ,求
,求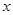 的值(用
的值(用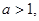 且
且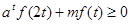 对于
对于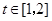 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用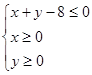 内随机任取一点(a,b).求函数y=f(x)在区间[1,+∞)上是增函数的概率.
内随机任取一点(a,b).求函数y=f(x)在区间[1,+∞)上是增函数的概率.