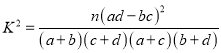题目内容
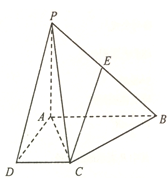
【题目】设函数
，函数
．
（1）求函数
的值域；
（2）若对于任意的
，总存在
，使得
成立，求实数
的取值范围．
【答案】（1）
；（2）
．
【解析】试题分析：
（1）根据
和
三种情况分别求出
的取值范围，最后可得函数的值域为
。（2）由（1）知，函数
的值域
。由函数
上单调递增，可得函数
的值域
，“对于任意的
，总存在
，使得
成立”等价于
，并由此得到
，解得
即为所求。
试题解析：
（1）①当
时， 
，则函数
在（0,1）上单调递增，在
上单调递减，所以
。
②当
时， 
；
③当
时， 
，则函数
在
上单调递减，在
上单调递增，所以
。
综上可得
。
所以函数
的值域为
。
（2）由（1）知，函数
的值域
又函数
上单调递增，
∴
，即
，
∴函数
的值域
，
由题意得“对于任意的
，总存在
，使得
成立”等价于
，
∴
，
解得
．
∴实数
的取值范围为
.
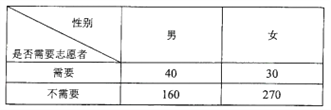
小学生10分钟口算测试100分系列答案
【题目】4月23日是世界读书日，惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位：分钟)的频率分布直方图，且将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”．
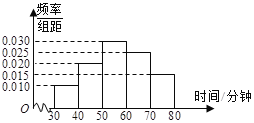
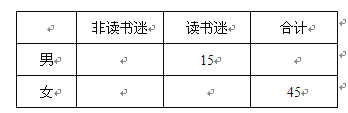
（Ⅰ）根据已知条件完成下面2×2列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？
（Ⅱ）将频率视为概率，现在从该校大量学生中用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中“读书迷”的人数为
，若每次抽取的结果是相互独立的，求
的分布列、数学期望
和方差
．
附：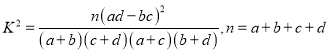 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】“累积净化量
”是空气净化器质量的一个重要衡量指标，它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示，根据
《空气净化器》国家标准，对空气净化器的累计净化量有如下等级划分：
累积净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器（共5000台）的质量，随机抽取
台机器作为样本进行估计，已知这台机器的累积净化量都分布在区间
中，按照
、
、
、
、
均匀分组，其中累积净化量在的所有数据有：4.5,4.6,5.2,5.3,5.7和5.9，并绘制了频率分布直方图，如图所示：
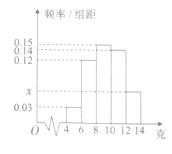
（1）求的值及频率分布直方图中
的值；
（2）以样本估计总体，试估计这批空气净化器（共5000台）中等级为
的空气净化器有多少台？
（3）从累积净化量在的样本中随机抽取2台，求恰好有1台等级为的概率.
【题目】某品牌汽车的
店，对最近100份分期付款购车情况进行统计，统计情况如下表所示.已知分9期付款的频率为0.4；该店经销一辆该品牌汽车，若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
（1）若以上表计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3为顾客，求事件
：“至多有1位采用分6期付款“的概率
；
（2）按分层抽样方式从这100为顾客中抽取5人，再从抽取的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量
，求
的分布列和数学期望
.
