题目内容
【题目】本市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼.摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:
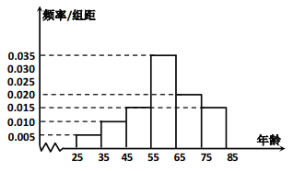
(1)根据频率分布直方图,求这100位摄影者年龄的样本平均数![]() 和中位数
和中位数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中评出20个最佳作品,并邀请作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组应抽取的人数;
年龄 |
|
|
|
|
|
|
人数 |
②若从较年轻的前三组作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在![]() 的概率.
的概率.
【答案】(1)平均数60,中位数![]() (2)①详见解析;②
(2)①详见解析;②![]() .
.
【解析】
(1)利用每组中点值作为代表,分别乘以频率然后相加,求得样本的平均数.根据面积之和为![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.(2)根据比例求得分层抽样每组应抽取的人数.利用列举法和古典概型概率计算公式,计算出所求的概率.
的值.(2)根据比例求得分层抽样每组应抽取的人数.利用列举法和古典概型概率计算公式,计算出所求的概率.
解:(1)在频率分布直方图中,这100位参赛者年龄的样本平均数
![]()
![]() .
.
设中位数为![]() ,由
,由![]() ,解得
,解得![]() (或答55.57).
(或答55.57).
(2)每组应各抽取人数如下表:
年龄 |
|
|
|
|
|
|
抽取人数 | 1 | 2 | 3 | 7 | 4 | 3 |
根据分层抽样的原理,年龄在前三组内分别有1人、2人、3人,设在第一组的是![]() ,在第二组的是
,在第二组的是![]() ,
,![]() ,在第三组的是
,在第三组的是![]() ,
,![]() ,
,![]() ,列举选出2人的所有可能如下:
,列举选出2人的所有可能如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共15种情况.
.共15种情况.
设“这2人至少有一人的年龄在区间![]() ”为事件
”为事件![]() ,所有可能如下:
,所有可能如下:
![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共9种情况.
共9种情况.
则![]() .
.

【题目】某市对各老旧小区环境整治效果进行满意度测评,共有10000人参加这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
组别 | 分组 | 频数 | 频率 |
1 |
| 3 | 0.06 |
2 |
| 15 | 0.3 |
3 |
| 21 |
|
4 |
| 3 | 0.12 |
5 |
|
| 0.1 |
合计 |
| 1.00 | |
(1)求出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若分数在80(含80分)以上表示对该项目“非常满意”,其中分数在90(含90分)以上表示“十分满意”,现从被抽取的“非常满意“人群中随机抽取2人,求至少有一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数