题目内容
16.设平面向量$\overrightarrow{a}$=($\sqrt{3}$,-1),$\overrightarrow{b}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),向量$\overrightarrow{c}$=$\overrightarrow{a}$+(tan2θ-1)$\overrightarrow{b}$,$\overrightarrow{d}$=tanθ$\overrightarrow{b}$,且$\overrightarrow{c}⊥\overrightarrow{d}$,当θ∈(-$\frac{π}{2}$,$\frac{π}{2}$)时,求θ值的集合.分析 求得$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{b}$|=1,再由向量垂直的条件:数量积为0,可得tanθ(tan2θ-1)=0,结合θ∈(-$\frac{π}{2}$,$\frac{π}{2}$),计算即可得到所求集合.
解答 解:$\overrightarrow{a}$=($\sqrt{3}$,-1),$\overrightarrow{b}$=($\frac{1}{2},\frac{\sqrt{3}}{2}$),
即有$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$=0,|$\overrightarrow{b}$|=1,
向量$\overrightarrow{c}$=$\overrightarrow{a}$+(tan2θ-1)$\overrightarrow{b}$,$\overrightarrow{d}$=tanθ$\overrightarrow{b}$,且$\overrightarrow{c}⊥\overrightarrow{d}$,
即有$\overrightarrow{c}$•$\overrightarrow{d}$=tanθ•$\overrightarrow{a}$•$\overrightarrow{b}$+tanθ(tan2θ-1)$\overrightarrow{b}$2=0,
则tanθ(tan2θ-1)=0,
即tanθ=0或±1,
当θ∈(-$\frac{π}{2}$,$\frac{π}{2}$)时,
即有θ=0或±$\frac{π}{4}$.
则θ的取值集合为{-$\frac{π}{4}$,0,$\frac{π}{4}$}.
点评 本题考查向量的数量积的坐标表示和性质,以及向量垂直的条件,考查运算能力,属于基础题.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案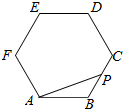 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].