题目内容
4.求使不等式a${\;}^{{x}^{2}-2x+1}$>a${\;}^{{x}^{2}-3x+5}$(a>0,且a≠1)成立的x的集合.分析 讨论a>1与1>a>0时,不等式的解集是什么,求出即可.
解答 解:∵不等式a${\;}^{{x}^{2}-2x+1}$>a${\;}^{{x}^{2}-3x+5}$(a>0,且a≠1),
∴a>1时,原不等式化为x2-2x+1>x2-3x+5,
解得x>4;
1>a>0时,原不等式化为x2-2x+1<x2-3x+5,
解得x<4;
综上,a>1时,不等式的解集为{x|x>4},
1>a>0时,不等式的解集为{x|x<4}.
点评 本题考查了指数函数的图象与性质的应用问题,也考查了不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
14.执行如图所示的程序框图,若输入x=4,则输出y的值为( )
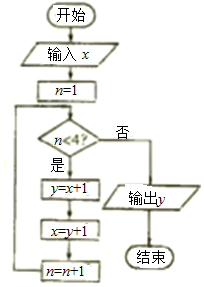

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
19.已知函数y=cos2x+bcosx(x∈R)的最小值为-3,则加入下列哪个条件,b的值是唯一的( )
| A. | b>-6 | B. | b<6 | C. | b≠4 | D. | b≠±4 |
16.对于定义域是R的任意奇函数f(x),都有( )
| A. | f(x)-f(-x)>0 | B. | f(x)-f(-x)≤0 | C. | f(x)•f(-x)≤0 | D. | f(x)•f(-x)>0 |
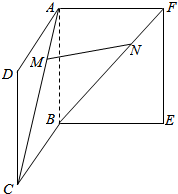 如图所示,已知正方形ABCD和ABEF,M、N是AC、BF上的点且AM=FN,求证:MN∥面BCE.
如图所示,已知正方形ABCD和ABEF,M、N是AC、BF上的点且AM=FN,求证:MN∥面BCE.