Question

8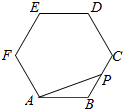．如图所示：点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动，其中AB=4，则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8，24]．

Answer 1

分析 如图所示，A（0，0），B（4，0），C$（6，2\sqrt{3}）$，D$（4，4\sqrt{3}）$，E（0，4$\sqrt{3}$），F$（-2，2\sqrt{3}）$．对点P分类讨论，利用数量积运算性质即可得出．

解答 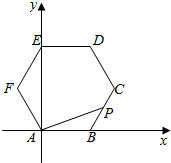解：如图所示，
A（0，0），B（4，0），C$（6，2\sqrt{3}）$，D$（4，4\sqrt{3}）$，E（0，4$\sqrt{3}$），F$（-2，2\sqrt{3}）$．
当点P位于线段AB上时，0≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤${\overrightarrow{AB}}^{2}$=16；
当点P位于线段BC上时，16=${\overrightarrow{AB}}^{2}$≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤$\overrightarrow{AC}•\overrightarrow{AB}$=24；
当点P位于线段CD上时，16=$\overrightarrow{AD}•\overrightarrow{AB}$≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤$\overrightarrow{AC}•\overrightarrow{AB}$=24；
当点P位于线段DE上时，0=$\overrightarrow{AB}•\overrightarrow{AE}$≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤$\overrightarrow{AD}•\overrightarrow{AB}$=16；
当点P位于线段EF上时，-8=$\overrightarrow{AF}•\overrightarrow{AB}$≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤$\overrightarrow{AC}•\overrightarrow{AB}$=$\overrightarrow{AE}•\overrightarrow{AB}$=0；
当点P位于线段FA上时，-8=$\overrightarrow{AF}•\overrightarrow{AB}$≤$\overrightarrow{AP}$•$\overrightarrow{AB}$≤0．
综上可得：$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[-8，24]．
故答案为：[-8，24]．

点评 本题考查了向量的数量积运算性质，考查了分类讨论方法、计算能力，属于中档题．