Question

【题目】（1）设a>b>0，试比较与的大小．

（2）若关于x的不等式(2x－1)2<ax2的解集中整数恰好有3个，求实数a的取值范围

Answer 1

【答案】（1）（2）

【解析】

(1)利用作差法或作商法证明即可.

(2)将不等式整理成二次不等式的形式,再根据解集中整数恰好有3个,分析二次方程的零点的范围即可知解集中整数解一定是1,2,3,再列出二次方程零点满足的范围即可.

解：（1）(作差法)

－＝

＝

＝．

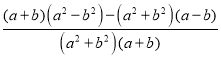
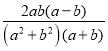∵a>b>0,∴a＋b>0,a－b>0,2ab>0,a2＋b2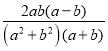>0,

∴>0,∴

(作商法)

∵a>b>0,∴>0, >0,2ab>0,

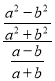∴＝＝＝1＋>1

(2)不等式(2x－1)2<ax2等价于(4－a)x2－4x＋1<0,∵不等式(2x－1)2<ax2的解集中整数恰好有3个,∴

解得0<a<4,

∴不等式的解集为<x<

∵<,

∴不等式(2x－1)2<ax2的解集中整数解一定是1,2,3,

∴3<≤4,解得<a≤,

∴a的取值范围