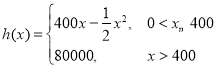题目内容
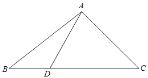
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(Ⅰ)在![]() 中,已知∠ADC=
中,已知∠ADC=![]() ,
,![]() ,要求sin∠DAC,所以将∠DAC用∠ADC和∠C来表示可得∠DAC=π﹣(∠ADC+∠C),进而用诱导公式可得
,要求sin∠DAC,所以将∠DAC用∠ADC和∠C来表示可得∠DAC=π﹣(∠ADC+∠C),进而用诱导公式可得![]() , 再用两角和的正弦公式展开,利用条件可求得结果;(Ⅱ)在△ABD中,知道一个角、两条边,故可用余弦定理求边AD的长。△ACD中,根据条件由正弦定理可求CD边长,进而可求BC边长,根据条件分别求
, 再用两角和的正弦公式展开,利用条件可求得结果;(Ⅱ)在△ABD中,知道一个角、两条边,故可用余弦定理求边AD的长。△ACD中,根据条件由正弦定理可求CD边长,进而可求BC边长,根据条件分别求![]() 的面积即可得所求。
的面积即可得所求。
解:(Ⅰ)△ACD中,因为∠DAC=π﹣(∠ADC+∠C),∠ADC=![]() ,
,
所以 ![]() =
=![]() ;
;
因为 ![]() ,0<∠C<π,所以
,0<∠C<π,所以 ![]() ;
;
所以 ![]() ;
;
(Ⅱ)在△ABD中,由余弦定理可得AB2=BD2+AD2﹣2BDADcos∠ADB,
所以 ![]() ,所以 AD2+6AD﹣160=0,即 (AD+16)(AD﹣10)=0,
,所以 AD2+6AD﹣160=0,即 (AD+16)(AD﹣10)=0,
解得AD=10或AD=﹣16(不合题意,舍去);所以 AD=10;
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,即
,即 ![]() ,解得CD=15;所以
,解得CD=15;所以 ![]() ,即
,即![]() .
.

【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间![]() (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 | 2 | 18 | 20 | 10 |
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.
分.
(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;
(分)的函数关系式;
(2)若王先生一次开车时间不超过40分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求![]() 的分布列和期望;
的分布列和期望;
(3)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了30名同学,得到如下的![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用智能手机的20名同学中,按分层抽样的方法选出5名同学,求所抽取的5名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中被抽取的5名同学,再随机抽取3名同学,试求抽取3名同学中恰有2名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |