题目内容
【题目】已知曲线
在
处的切线方程为
.
（Ⅰ）求
值.
（Ⅱ）若函数
有两个零点，求实数
的取值范围.
【答案】(Ⅰ)
；(Ⅱ)
【解析】
（Ⅰ）利切点
为曲线
和直线
的公共点，得出
，并结合
列方程组求出实数
、
的值；
（Ⅱ）解法1：由
，得出
，将问题转化为直线
与曲线
的图象有两个交点时，求出实数
的取值范围，然后利用导数研究函数
的单调性与极值，借助数形结合思想得出实数的取值范围；
解法2：利用导数得出函数
的极小值为
，并利用极限思想得出当
时，
，结合题意得出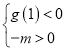
，从而得出实数的取值范围。
（Ⅰ）
，
，
；
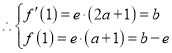
（Ⅱ）解法1：
，
函数
有两个零点，相当于曲线
与直线有两个交点.
，
当
时，
在
单调递减，
当
时，
在
单调递增，
时，
取得极小值
，
又
时，
；
时，
，
；
解法2：，
，
当时，
在上单调递减，
当时，
在上单调递增，
时，
取得极小值
，
又时，，
.
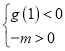
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响，询问了30名同学，得到如下的
列联表：
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
（Ⅰ）根据以上列联表判断，能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响？
（Ⅱ）从使用智能手机的20名同学中，按分层抽样的方法选出5名同学，求所抽取的5名同学中“学习成绩优秀”和“学习成绩不优秀”的人数；
（Ⅲ）从问题（Ⅱ）中被抽取的5名同学，再随机抽取3名同学，试求抽取3名同学中恰有2名同学为“学习成绩不优秀”的概率.
参考公式：
，其中
参考数据：
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】夏天喝冷饮料已成为年轻人的时尚. 某饮品店购进某种品牌冷饮料若干瓶，再保鲜.
（Ⅰ）饮品成本由进价成本和可变成本（运输、保鲜等其它费用）组成.根据统计，“可变成本”
（元）与饮品数量
（瓶）有关系.与之间对应数据如下表：
饮品数量 | 2 | 4 | 5 | 6 | 8 |
可变成本 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据，用最小二乘法求出关于的线性回归方程
；如果该店购入20瓶该品牌冷饮料，估计“可变成本”约为多少元？
（Ⅱ）该饮品店以每瓶10元的价格购入该品牌冷饮料若干瓶，再以每瓶15元的价格卖给顾客。如果当天前8小时卖不完，则通过促销以每瓶5元的价格卖给顾客(根据经验，当天能够把剩余冷饮料都低价处理完毕，且处理完毕后，当天不再购进)．该店统计了去年同期100天该饮料在每天的前8小时内的销售量(单位：瓶)，制成如下表：
每日前8个小时 销售量（单位：瓶） | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | 15 | 16 | 16 | 15 | 13 | 15 |
若以100天记录的频率作为每日前8小时销售量发生的概率，若当天购进18瓶，求当天利润的期望值.
（注：利润=销售额
购入成本 “可变本成”）
参考公式：回归直线方程为，其中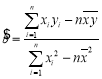
参考数据：
， 
.
