题目内容
【题目】在平面直角坐标系xOy中,点A(1,0),动点M满足以MA为直径的圆与y轴相切.过A作直线x+(m﹣1)y+2m﹣5=0的垂线,垂足为B,则|MA|+|MB|的最小值为( )
A.2![]() B.2
B.2![]() C.
C.![]() D.3
D.3![]()
【答案】D
【解析】
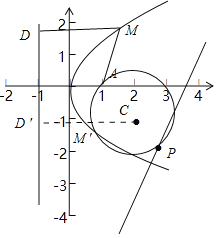
根据题意,设M(x,y),求出![]() 点轨迹方程y2=4x,即可得M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,过点M作MD与准线垂直,且交准线于点D,分析可得直线x+(m﹣1)y+2m﹣5=0经过定点(3,﹣2),设P(3,-2),由点
点轨迹方程y2=4x,即可得M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,过点M作MD与准线垂直,且交准线于点D,分析可得直线x+(m﹣1)y+2m﹣5=0经过定点(3,﹣2),设P(3,-2),由点![]() 性质可得B在以AP为直径的圆上,由抛物线的定义可得又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,通过
性质可得B在以AP为直径的圆上,由抛物线的定义可得又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,通过![]() (
(![]() 为
为![]() 中点,圆心)结合图形分析可得答案.
中点,圆心)结合图形分析可得答案.
根据题意,设M(x,y),以MA为直径的圆的圆心为(![]() ,
,![]() ),
),
又由动点M满足以MA为直径的圆与y轴相切,则有(![]() )2=(
)2=(![]() 1)2+(
1)2+(![]() )2,
)2,
变形可得:y2=4x,
则M的轨迹是抛物线,其焦点为A(1,0),准线为x=﹣1,
过点M作MD与准线垂直,且交准线于点D,
设直线l为x+(m﹣1)y+2m﹣5=0,变形可得m(y+2)=y﹣x+5,
∴可得直线l经过定点(3,﹣2),
设P(3,-2),设AP的中点为C,则C的坐标为(2,﹣1),|CP|![]() ,
,
若AB⊥l,则B在以AP为直径的圆上,该圆的方程为![]() ,
,
又由|MA|=|MD|,则|MA|+|MB|=|MD|+|MB|,
则当C、M、D三点共线时,|MA|+|MB|取得最小值,且|MA|+|MB|取得最小值为圆![]() 上的点到D的最小值,
上的点到D的最小值,
此时|MA|+|MB|min=|CD|﹣r=3![]() ,
,
故选:D.

练习册系列答案
相关题目