题目内容
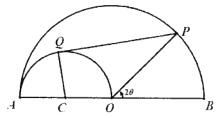
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]()
【解析】
(1)由题意,结合三角恒等变换的公式,求得![]() ,再利用三角函数的性质,即可求解;
,再利用三角函数的性质,即可求解;
(2)由题意,取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,求得弧长
,求得弧长![]() 和线段
和线段![]() 的长度之和表达式
的长度之和表达式![]() ,设
,设![]() ,
,![]() ,得到
,得到![]() ,结合导数求得函数的单调性和最值,即可求解.
,结合导数求得函数的单调性和最值,即可求解.
(1)由题意,在![]() 中,可得
中,可得![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
所以![]()
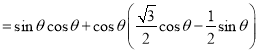
![]()
![]()
![]() .
.
因为![]() ,则
,则![]() ,
,
所以当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值,且最大值为
取得最大值,且最大值为![]() 千米.
千米.
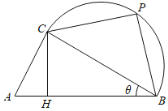
(2)取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
由(1)知,![]() ,
,![]()
故![]() 的长为
的长为![]() ,
,
则![]() 和线段
和线段![]() 的长度之和
的长度之和
![]()
![]() ,
,![]() .
.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,故
上单调递减,故![]() .
.
易知函数![]() 在区间
在区间![]() 上也单调递减,所以
上也单调递减,所以![]() ,
,
所以![]() ,
,
所以当且仅当![]() 时,
时,![]() 和线段
和线段![]() 的长度之和最大.
的长度之和最大.

 阅读快车系列答案
阅读快车系列答案【题目】呼和浩特市地铁一号线于2019年12月29日开始正式运营有关部门通过价格听证会,拟定地铁票价后又进行了一次调查.调查随机抽查了50人,他们的月收入情况与对地铁票价格态度如下表:
月收入(单位:百元) |
|
|
|
|
|
|
认为票价合理的人数 | 1 | 2 | 3 | 5 | 3 | 4 |
认为票价偏高的人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)若以区间的中点值作为月收入在该区间内人的人均月收入求参与调查的人员中“认为票价合理者”的月平均收入与“认为票价偏高者”的月平均收入的差是多少(结果保留2位小数);
(2)由以上统计数据填写下面![]() 列联表分析是否有
列联表分析是否有![]() 的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
的把握认为“月收入以5500元为分界点对地铁票价的态度有差异”
月收入不低于5500元人数 | 月收入低于5500元人数 | 合计 | |
认为票价偏高者 | |||
认为票价合理者 | |||
合计 |
附:![]()
| 0.05 | 0.01 |
| 3.841 | 6.635 |