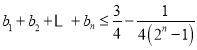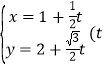题目内容
【题目】已知圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 的准线
的准线![]() 相切.
相切.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,若
,若![]() 的面积为6,求直线
的面积为6,求直线![]() 的方程.
的方程.
【答案】(1)y2=4x.(2)2x±3y﹣2=0.
【解析】
(1)根据抛物线的定义即可得解;
(2)设A(x1,y1),B(x2,y2),则C(x2,﹣y2),由抛物线的定义可知,|AF|=x1+1,|CF|=x2+1.设直线AB的方程为y=k(x﹣1),将其与抛物线的方程联立,消去y可得关于x的一元二次方程,写出韦达定理;设直线m(AB)的倾斜角为α,则tanα=k,且sin∠AFC=|sin(π﹣2α)|=|sin2α|=2sinαcosα,将其转化为只含k的代数式,再利用正弦面积公式得,![]() ,结合韦达定理表达式,化简整理可得
,结合韦达定理表达式,化简整理可得![]() ,从而解出k的值,进而求得直线m的方程.
,从而解出k的值,进而求得直线m的方程.
(1)由已知可得:圆心(4,4)到焦点F的距离与到准线l的距离相等,即点(4,4)在抛物线E上,
∴16=8p,解得p=2.
∴抛物线E的标准方程为y2=4x.
(2)由已知可得,直线m斜率存在,否则点C与点A重合.
设直线m的斜率为k(k≠0),则直线AB的方程为y=k(x﹣1).
设A(x1,y1),B(x2,y2),
联立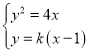 消去y得k2x2﹣2(k2+2)x+k2=0.
消去y得k2x2﹣2(k2+2)x+k2=0.
∴![]() ,x1x2=1.
,x1x2=1.
由对称性可知,C(x2,﹣y2),∴|AF|=x1+1,|CF|=x2+1.
设直线m(AB)的倾斜角为α,则tanα=k,
∴![]() ,
,
∴![]() .
.
由已知可得![]() ,解得
,解得![]() .
.
∴直线m的方程为![]() ,即2x±3y﹣2=0.
,即2x±3y﹣2=0.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目