题目内容
【题目】在平面直角坐标系x0y中,已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ),E为动点,且直线EA与直线EB的斜率之积为﹣
),E为动点,且直线EA与直线EB的斜率之积为﹣ ![]() . (Ⅰ)求动点E的轨迹C的方程;
. (Ⅰ)求动点E的轨迹C的方程;
(Ⅱ)设过点F(1,0)的直线l与曲线C相交于不同的两点M,N.若点P在y轴上,且|PM|=|PN|,求点P的纵坐标的取值范围.
【答案】解:(Ⅰ)设动点E的坐标为(x,y), ∵点A(﹣ ![]() ,0),B(
,0),B( ![]() ),E为动点,且直线EA与直线EB的斜率之积为﹣
),E为动点,且直线EA与直线EB的斜率之积为﹣ ![]() ,
,
∴ ![]() ,
,
整理,得 ![]() ,x≠
,x≠ ![]() ,
,
∴动点E的轨迹C的方程为 ![]() ,x
,x ![]() .
.
(Ⅱ)当直线l的斜率不存在时,满足条件的点P的纵坐标为0,
当直线l的斜率存在时,设直线l的方程为y=k(x﹣1),
将y=k(x﹣1)代入 ![]() ,并整理,得
,并整理,得
(2k2+1)x2﹣4k2x+2k2﹣2=0,
△=8k2+8>0,
设M(x1 , y1),N(x2 , y2),则 ![]() ,x1x2=
,x1x2= ![]() ,
,
设MN的中点为Q,则 ![]() ,
, ![]() ,
,
∴Q( ![]() ,﹣
,﹣ ![]() ),
),
由题意知k≠0,
又直线MN的垂直平分线的方程为y+ ![]() =﹣
=﹣ 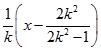 ,
,
令x=0,得yP= 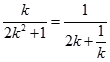 ,
,
当k>0时,∵2k+ ![]()
![]() ,∴0<
,∴0< ![]() ;
;
当k<0时,因为2k+ ![]() ≤﹣2
≤﹣2 ![]() ,所以0>yP≥﹣
,所以0>yP≥﹣ ![]() =﹣
=﹣ ![]() .
.
综上所述,点P纵坐标的取值范围是[﹣ ![]() ]
]
【解析】(Ⅰ)设动点E的坐标为(x,y),由点A(﹣ ![]() ,0),B(
,0),B( ![]() ),E为动点,且直线EA与直线EB的斜率之积为﹣
),E为动点,且直线EA与直线EB的斜率之积为﹣ ![]() ,知
,知 ![]() ,由此能求出动点E的轨迹C的方程.(Ⅱ)设直线l的方程为y=k(x﹣1),将y=k(x﹣1)代入
,由此能求出动点E的轨迹C的方程.(Ⅱ)设直线l的方程为y=k(x﹣1),将y=k(x﹣1)代入 ![]() ,得(2k2+1)x2﹣4k2x+2k2﹣2=0,由题设条件能推导出直线MN的垂直平分线的方程为y+
,得(2k2+1)x2﹣4k2x+2k2﹣2=0,由题设条件能推导出直线MN的垂直平分线的方程为y+ ![]() =﹣
=﹣ ![]() ,由此能求出点P纵坐标的取值范围.
,由此能求出点P纵坐标的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目