题目内容
【题目】已知函数f(x)= ![]() ,(x>0且a≠1)的图象经过点(﹣2,3).
,(x>0且a≠1)的图象经过点(﹣2,3). 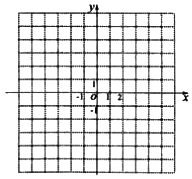
(Ⅰ)求a的值,并在给出的直角坐标系中画出y=f(x)的图象;
(Ⅱ)若f(x)在区间(m,m+1)上是单调函数,求m的取值范围.
【答案】解:(Ⅰ)∵函数的图象经过点(﹣2,3),∴a﹣2﹣1=3,解得 ![]() ,
,
∴ 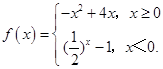
其图象如图所示: 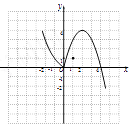
(Ⅱ)由(Ⅰ)可知函数的单调递增区间是(0,2),单调递减区间是(﹣∞,0),(2,+∞),
∴m+1≤0或m≥2或 ![]() ,
,
∴m的取值范围为m≤﹣1或0≤m≤1或m≥2.
【解析】(Ⅰ)利用函数的图象经过点(﹣2,3),求出a,得到函数解析式,然后画出图象.(Ⅱ)由(Ⅰ)可知函数的图象,可知函数的单调递增区间是(0,2),单调递减区间是(﹣∞,0),(2,+∞),推出m的取值范围.
【考点精析】解答此题的关键在于理解函数的图象的相关知识,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目