题目内容
【题目】如图，在直三棱柱ABC﹣A1B1C1中，三角形ABC为等腰直角三角形，AC=BC= 
，AA1=1，点D是AB的中点．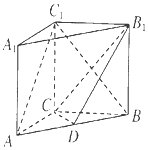 
（1）求证：AC1∥平面CDB1；
（2）二面角B1﹣CD﹣B的平面角的大小．
【答案】
（1）证明：在直三棱柱ABC﹣A1B1C1中，
设BC1∩B1C=E，则E为BC1的中点，连接ED
∵D为AB的中点，∴ED∥AC
又∵ED平面CDB1，AC1平面CDB1，
∴AC1∥平面CDB1．
（2）解：∵△ABC中，AC=BC，D为AB中点，∴CD⊥AB，
又∵BB1⊥平面ABC，CD平面ABC，∴BB1⊥CD，
又AB∩BB1=B，∴CD⊥平面ABB1A1，
∵B1D平面ABB1A1，AB平面ABB1A1
∴CD⊥B1D，CD⊥AB，
∴∠B1DB为二面角B1﹣CD﹣B的平面角
∵三角形ABC中，AB=2，∴BD=1，
在Rt△B1BD中， 
，
∴∠B1BD=45°，
∴二面角B1﹣CD﹣B的平面角的大小为45°．
【解析】（1）设BC1∩B1C=E，连接ED，则ED∥AC，由此能证明AC1∥平面CDB1．（2）推导出CD⊥AB，BB1⊥CD，从而CD⊥平面ABB1A1，进而CD⊥B1D，CD⊥AB，∠B1DB为二面角B1﹣CD﹣B的平面角，由此能求出二面角B1﹣CD﹣B的平面角的大小．
【考点精析】关于本题考查的直线与平面平行的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．
练习册系列答案
相关题目
