题目内容
已知函数f(x)=ax2+bln x在x=1处有极值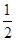 .
.
(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
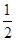 .
.(1)求a,b的值;
(2)判断函数y=f(x)的单调性并求出单调区间.
(1) 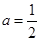 ,
,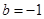 (2) 单调减区间是
(2) 单调减区间是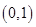 ,单调增区间是
,单调增区间是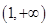
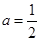 ,
,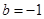 (2) 单调减区间是
(2) 单调减区间是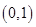 ,单调增区间是
,单调增区间是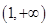
试题分析:(1) 先求导,根据已知条件可得
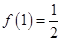 且
且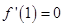 ,解方程组可得
,解方程组可得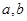 的值。(2)由(1)可知
的值。(2)由(1)可知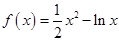 ,先求导并将其同分整理,令导数大于0可得增区间,令导数小于0得减区间。
,先求导并将其同分整理,令导数大于0可得增区间,令导数小于0得减区间。(1)
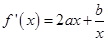 .
.又
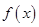 在
在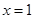 处有极值
处有极值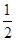 .
.∴
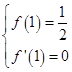 即
即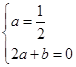
解之得
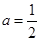 且
且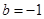 .
.(2)由(1)可知
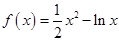 ,其定义域是
,其定义域是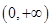 ,
,且
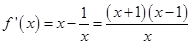 .
.由
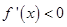 ,得
,得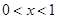 ;
;由
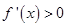 ,得
,得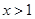 .
.所以函数
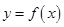 的单调减区间是
的单调减区间是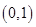 ,单调增区间是
,单调增区间是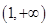 .
.
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
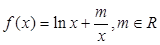 .
.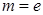 (
(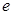 为自然对数的底数)时,求
为自然对数的底数)时,求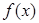 的最小值;
的最小值;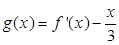 零点的个数;
零点的个数;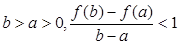 恒成立,求
恒成立,求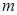 的取值范围.
的取值范围.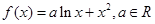
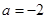 ,求证:函数
,求证:函数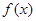 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;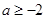 时,求函数
时,求函数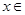 [l,e],使得
[l,e],使得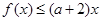 成立,求实数
成立,求实数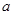 的取值范围.
的取值范围.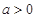 ,函数
,函数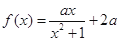 ,
,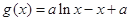 .
. 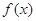 的单调区间;
的单调区间;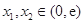 ,都有
,都有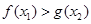 .
.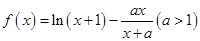 .
.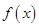 的单调性;
的单调性;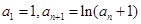 ,证明:
,证明: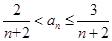 .
.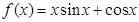 的导函数原点处的部分图象大致为 ( )
的导函数原点处的部分图象大致为 ( )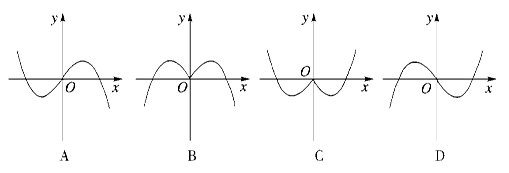
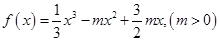 。
。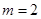 时,①求函数
时,①求函数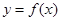 的单调区间;②求函数
的单调区间;②求函数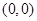 处的切线方程;
处的切线方程;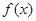 既有极大值,又有极小值,且当
既有极大值,又有极小值,且当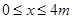 时,
时,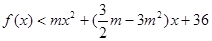 恒成立,求
恒成立,求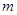 的取值范围.
的取值范围.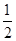 x-
x-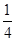 sinx-
sinx-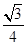 cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.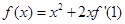 ,则
,则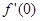 = .
= .