题目内容
已知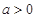 ,函数
,函数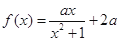 ,
,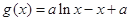 .
.
(1)求函数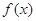 的单调区间;
的单调区间;
(2)求证:对于任意的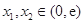 ,都有
,都有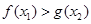 .
.
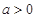 ,函数
,函数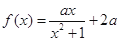 ,
,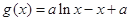 .
. (1)求函数
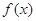 的单调区间;
的单调区间;(2)求证:对于任意的
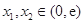 ,都有
,都有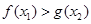 .
.(1)单调递增区间为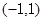 ,单调递减区间为
,单调递减区间为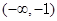 ,
,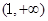 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
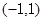 ,单调递减区间为
,单调递减区间为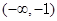 ,
,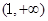 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先对
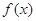 求导,利用
求导,利用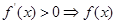 单调递增,
单调递增,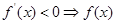 单调递减,通过解不等式,求出函数
单调递减,通过解不等式,求出函数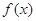 的单调区间;第二问,由于对于任意的
的单调区间;第二问,由于对于任意的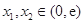 ,都有
,都有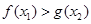
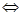 对于任意的
对于任意的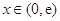 ,都有
,都有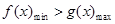 ,利用导数判断函数
,利用导数判断函数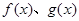 在
在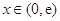 上的单调性,数形结合求出
上的单调性,数形结合求出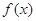 的最小值和
的最小值和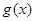 的最大值,进行比较,看是否符合
的最大值,进行比较,看是否符合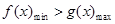 .
.(1)函数
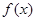 的定义域为
的定义域为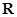 ,
,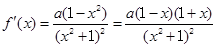 ,
,因为
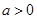 ,
,所以,当
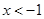 ,或
,或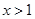 时,
时,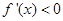 ;
; 当
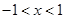 时,
时,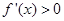 .
.所以,
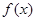 的单调递增区间为
的单调递增区间为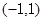 ,单调递减区间为
,单调递减区间为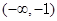 ,
,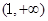 . 6分
. 6分(2)因为
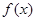 在区间
在区间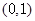 上单调递增,在区间
上单调递增,在区间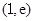 上单调递减,
上单调递减,又
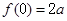 ,
,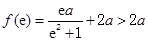 ,
,所以,当
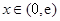 时,
时,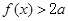 .
.由
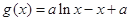 ,可得
,可得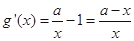 .
.所以当
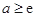 时,函数
时,函数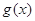 在区间
在区间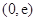 上是增函数,
上是增函数,所以,当
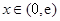 时,
时,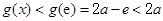 .
.所以,当
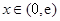 时,
时,对于任意的
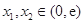 ,都有
,都有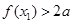 ,
,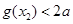 ,所以
,所以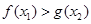 .
.当
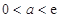 时,函数
时,函数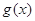 在区间
在区间 上是增函数,在区间
上是增函数,在区间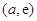 上是减函数,
上是减函数,所以,当
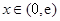 时,
时,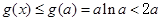 .
.所以,当
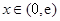 时,
时,对于任意的
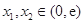 ,都有
,都有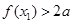 ,
,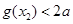 ,所以
,所以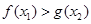 .
.综上,对于任意的
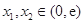 ,都有
,都有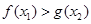 . 13分
. 13分
练习册系列答案
相关题目
 ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.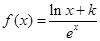 (其中
(其中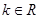 ),
),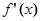 为f(x)的导函数.
为f(x)的导函数.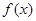 在点(1,
在点(1,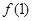 )处的切线不过点(2,0);
)处的切线不过点(2,0);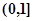 中存在
中存在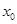 ,使得
,使得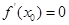 ,求
,求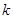 的取值范围;
的取值范围;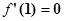 ,试证明:对任意
,试证明:对任意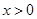 ,
,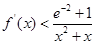 恒成立.
恒成立.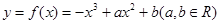
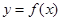 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;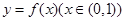 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求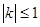 的充要条件;
的充要条件;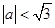 .
.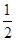 .
. )是定义在(一
)是定义在(一 ,0)上的可导函数,其导函数为
,0)上的可导函数,其导函数为 ,且有
,且有 ,则不等式
,则不等式 的解集为-------------
的解集为------------- 在
在 处有极大值,则常数
处有极大值,则常数 的值为_________.
的值为_________. ,若
,若 ,则
,则 ( )
( )


