题目内容
6.在($\sqrt{x}-\frac{2}{\sqrt{x}}$)n的展开式中,偶数项的二次项系数为64,则展开式共有( )| A. | 6项 | B. | 7项 | C. | 8项 | D. | 9项 |
分析 偶数项的二次项系数为2n-1=64,求得n的值,可得展开式的项数.
解答 解:在($\sqrt{x}-\frac{2}{\sqrt{x}}$)n的展开式中,偶数项的二次项系数为2n-1=64,n=7,
故展开式共有8项,
故选:C.
点评 本题主要考查二项式定理的应用,二项式系数的性质,注意各项系数和与各项的二项式系数和的区别,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
16.半径为1的球内最大圆柱的体积为( )
| A. | $\frac{2\sqrt{6}}{9}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{2\sqrt{3}}{3}$π | D. | $\frac{4\sqrt{3}}{9}$π |
9.若向量$\overrightarrow a$=(1,2),$\overrightarrow{b}$=(1,-1),则2$\overrightarrow a$+$\overrightarrow{b}$与$\overrightarrow a$-$\overrightarrow{b}$的夹角等于( )
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
 如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.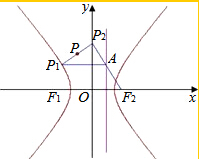 已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.
已知点P1(x0,y0)为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b为正常数)上任一点,F2为双曲线的右焦点,过P作直线x=$\frac{8b}{3}$的垂线,垂足为A,连接F2A并延长交y轴于P2.