题目内容
已知三次函数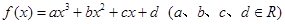 为奇函数,且在点
为奇函数,且在点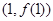 的切线方程为
的切线方程为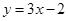
(1)求函数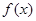 的表达式;
的表达式;
(2)已知数列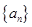 的各项都是正数,且对于
的各项都是正数,且对于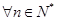 ,都有
,都有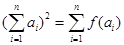 ,求数列
,求数列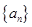 的首项
的首项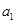 和通项公式;
和通项公式;
(3)在(2)的条件下,若数列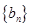 满足
满足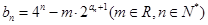 ,求数列
,求数列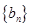 的最小值.
的最小值.
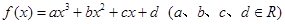 为奇函数,且在点
为奇函数,且在点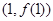 的切线方程为
的切线方程为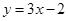
(1)求函数
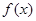 的表达式;
的表达式;(2)已知数列
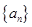 的各项都是正数,且对于
的各项都是正数,且对于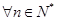 ,都有
,都有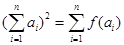 ,求数列
,求数列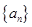 的首项
的首项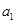 和通项公式;
和通项公式;(3)在(2)的条件下,若数列
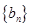 满足
满足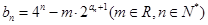 ,求数列
,求数列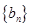 的最小值.
的最小值.(1)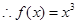 (2)
(2)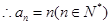
(3)①若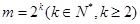 时, 数列
时, 数列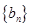 的最小值为当
的最小值为当 时,
时,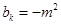
②若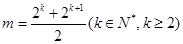 时, 数列
时, 数列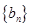 的最小值为, 当
的最小值为, 当 时或
时或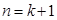
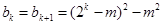
③若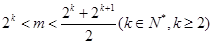 时, 数列
时, 数列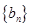 的最小值为,当
的最小值为,当 时,
时,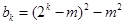
④若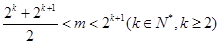 时,数列
时,数列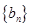 的最小值为,当
的最小值为,当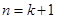 时
时
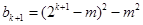
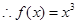 (2)
(2)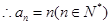
(3)①若
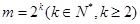 时, 数列
时, 数列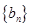 的最小值为当
的最小值为当 时,
时,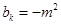
②若
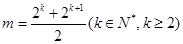 时, 数列
时, 数列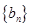 的最小值为, 当
的最小值为, 当 时或
时或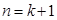
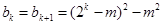
③若
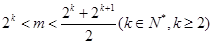 时, 数列
时, 数列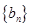 的最小值为,当
的最小值为,当 时,
时,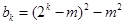
④若
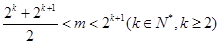 时,数列
时,数列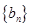 的最小值为,当
的最小值为,当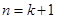 时
时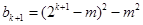
试题分析:解:(1) ∵
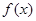 为奇函数,
为奇函数, 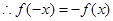 ,
,即
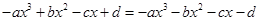
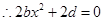
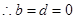 3分
3分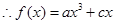 ,又因为在点
,又因为在点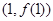 的切线方程为
的切线方程为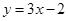
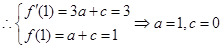 ,
,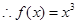 4分
4分(2)由题意可知:
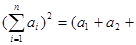 ....
....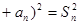
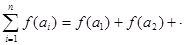
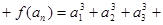 +
+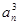
所以
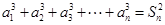 ①
①由①式可得
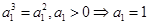 5分
5分当
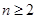 ,
,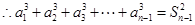 ②
②由①-②可得:

∵
 为正数数列
为正数数列 ..③ 6分
..③ 6分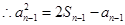 ④
④由③-④可得:

∵
 >0,
>0,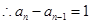 ,
,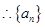 是以首项为1,公差为1的等差数列, 8分
是以首项为1,公差为1的等差数列, 8分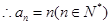 9分
9分(注意:学生可能通过列举然后猜测出
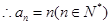 ,扣2分,即得7分)
,扣2分,即得7分)(3) ∵
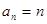
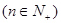 ,
,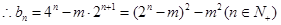
令
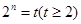 ,
,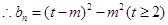 10分
10分(1)当
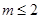 时,数列
时,数列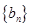 的最小值为当
的最小值为当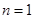 时,
时,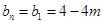 11分
11分(2)当
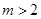 时
时①若
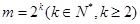 时, 数列
时, 数列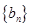 的最小值为当
的最小值为当 时,
时,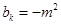
②若
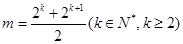 时, 数列
时, 数列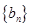 的最小值为, 当
的最小值为, 当 时或
时或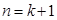
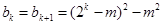
③若
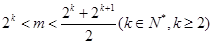 时, 数列
时, 数列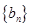 的最小值为,当
的最小值为,当 时,
时,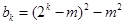
④若
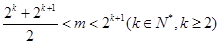 时,数列
时,数列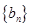 的最小值为,当
的最小值为,当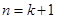 时
时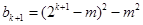 14分
14分点评:解决的关键是根据数列的性质以及数列的前n想项和与通项公式的关系来求解,属于基础题。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为 .
.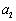 ,
, ,
,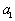 成等比数列,求数列
成等比数列,求数列 的前
的前 项和.
项和.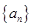 是等差数列,它的前
是等差数列,它的前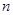 项和
项和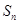 满足:
满足: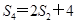 ,令
,令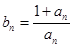 .若对任意的
.若对任意的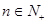 ,都有
,都有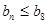 成立,则
成立,则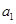 的取值范围是
的取值范围是 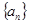 的前
的前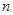 项和为
项和为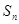 ,已知
,已知 ,
,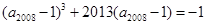 ,则下列结论中正确的是( )
,则下列结论中正确的是( )



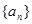 中,已知前
中,已知前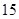 项的和
项的和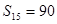 ,则
,则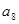 等于
等于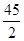
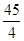
 中,若
中,若 ,则
,则 。
。 的前n项和是
的前n项和是 ,且
,且 则
则 .
.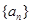 中,首项a1=1,公差d为整数,且满足
中,首项a1=1,公差d为整数,且满足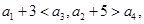 数列
数列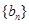 满足
满足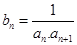 前
前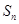 .
.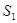 ,
,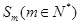 的等比中项,求正整数m的值.
的等比中项,求正整数m的值.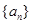 、
、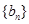 的前项和分别为
的前项和分别为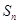 、
、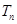 ,对任意的
,对任意的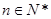 都有
都有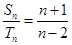 ,则
,则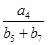
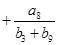 = .
= .