题目内容
设等差数列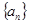 的前
的前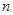 项和为
项和为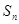 ,已知
,已知 ,
,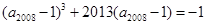 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
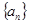 的前
的前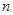 项和为
项和为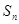 ,已知
,已知 ,
,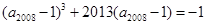 ,则下列结论中正确的是( )
,则下列结论中正确的是( )A. | B. |
C. | D. |
A
试题分析:先确定等差数列的公差d<0,再将条件相加,结合等差数列的求和公式及等差数列的性质,即可求得结论解:由
 ,
,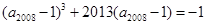 ,可得a6-1>0,-1<a2006-1<0,即a6>1,0<a2006<1,从而可得等差数列的公差d<0,∴a2016<a6,把已知的两式相加可得(a6-1)3+2012(a6-1)+(a2008-1)3+2012(a2008-1)=0整理可得(a6+a2008-2)•[(a6-1)2+(a2006-1)2-(a6-1)(a2006-1)+2013]=0,结合上面的判断可知(a6-1)2+(a2008-1)2-(a6-1)(a2008-1)+2012>0,所以a6+a2008=2,而
,可得a6-1>0,-1<a2006-1<0,即a6>1,0<a2006<1,从而可得等差数列的公差d<0,∴a2016<a6,把已知的两式相加可得(a6-1)3+2012(a6-1)+(a2008-1)3+2012(a2008-1)=0整理可得(a6+a2008-2)•[(a6-1)2+(a2006-1)2-(a6-1)(a2006-1)+2013]=0,结合上面的判断可知(a6-1)2+(a2008-1)2-(a6-1)(a2008-1)+2012>0,所以a6+a2008=2,而 ,故选A.
,故选A.点评:本题考查了等差数列的性质的运用,灵活利用等差数列的性质是解决问题的关键,属于中档题

练习册系列答案
相关题目
 的前
的前 项和是
项和是 ,若
,若 (
( N*,且
N*,且 ),则必定有( )
),则必定有( ) ,且
,且
 ,且
,且
 中,
中,  则
则 ( )
( )
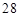

 是等差数列,
是等差数列,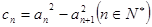
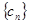 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;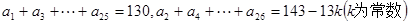 ,试写出数列
,试写出数列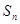 ,问是否存在这样的实数
,问是否存在这样的实数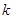 ,使
,使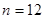 时取得最大值。若存在,求出
时取得最大值。若存在,求出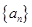 中,
中,
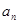 }{
}{ 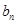 }的前n 项和为
}的前n 项和为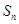 ,
,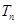 ,若
,若 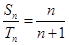 ,则
,则 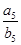 =
=

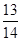

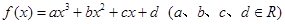 为奇函数,且在点
为奇函数,且在点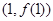 的切线方程为
的切线方程为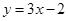
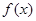 的表达式;
的表达式;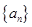 的各项都是正数,且对于
的各项都是正数,且对于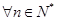 ,都有
,都有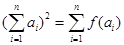 ,求数列
,求数列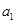 和通项公式;
和通项公式;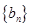 满足
满足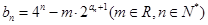 ,求数列
,求数列 ,若
,若 ,则
,则 ________.
________.