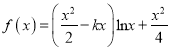题目内容
【题目】
的单调递减区间为 ．
【答案】[kπ﹣ 
，kπ+ 
]（k∈Z）
【解析】解：令t=sinxcosx+cos2x，则y= 
单调递减， t=sinxcosx+cos2x= 
+ 
sin（2x+ ）＞0，
令2kπ﹣ ≤2x+ ≤2kπ+ 
解得kπ﹣ ≤x≤kπ+ ，单调递增区间为[kπ﹣ ，kπ+ ]（k∈Z），
∴ 
的单调递减区间为[kπ﹣ ，kπ+ ]（k∈Z），
所以答案是[kπ﹣ ，kπ+ ]（k∈Z）．
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识，掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”，以及对正弦函数的单调性的理解，了解正弦函数的单调性：在
上是增函数；在
上是减函数．
练习册系列答案
阅读快车系列答案
相关题目
