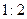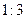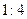题目内容
(本题12分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(1)求证: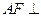 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.

如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(1)求证:
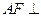 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.

略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;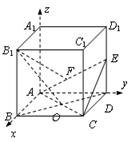
 a,AD
a,AD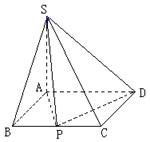
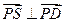 .
. 个单位法向量
个单位法向量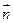
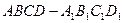 的底面为正方形,
的底面为正方形,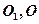 分别为上、下底面的中心,且
分别为上、下底面的中心,且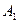 在底面
在底面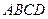 的射影是
的射影是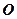 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面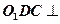 平面
平面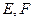 分别在棱上
分别在棱上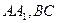 上,且
上,且 ,问点
,问点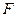 在何处时,
在何处时,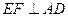 ;
;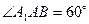 ,求二面角
,求二面角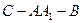 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。
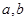 分别在平面
分别在平面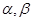 内,且平面
内,且平面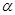 与
与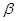 的交线为
的交线为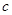 ,则直线
,则直线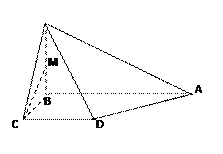
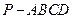 中,
中,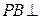 平面
平面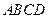 ,
, 底面
底面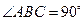 ,
,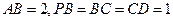 。
。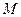 为
为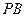 的中点,证明:直线
的中点,证明:直线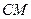 ∥平面
∥平面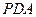 ;
;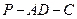 的余弦值。
的余弦值。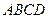 是边长为
是边长为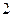 的正方形,
的正方形,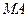 和
和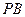 都与平面
都与平面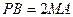
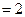 ,设平面
,设平面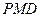 与平面
与平面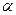 ,则
,则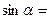 ▲
▲ 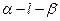 的大小是60°,线段
的大小是60°,线段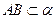 .
.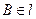 ,
,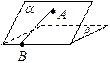
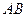 与
与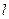 所成的角为30°.则
所成的角为30°.则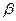 所成的角的正弦值是▲
所成的角的正弦值是▲ 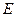 为正方体
为正方体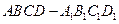 的棱
的棱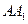 的中点,
的中点,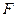 为棱
为棱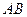 上一点,
上一点,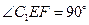 ,则
,则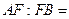 ( )
( )