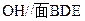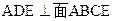题目内容
(本小题满分12分)
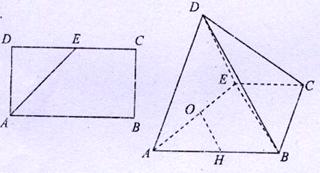
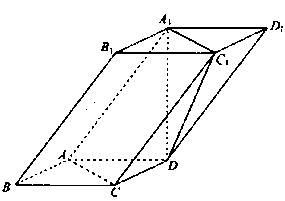
已知平行六面体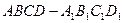 的底面为正方形,
的底面为正方形,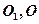 分别为上、下底面的中心,且
分别为上、下底面的中心,且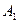 在底面
在底面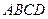 的射影是
的射影是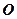 。
。
 (Ⅰ)求证:平面
(Ⅰ)求证:平面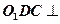 平面
平面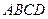 ;
;
(Ⅱ)若点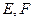 分别在棱上
分别在棱上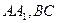 上,且
上,且 ,问点
,问点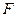 在何处时,
在何处时,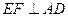 ;
;
(Ⅲ)若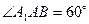 ,求二面角
,求二面角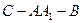 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。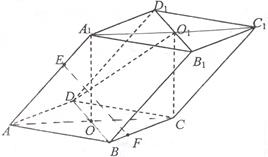
已知平行六面体
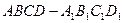 的底面为正方形,
的底面为正方形,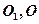 分别为上、下底面的中心,且
分别为上、下底面的中心,且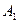 在底面
在底面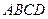 的射影是
的射影是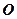 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面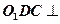 平面
平面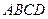 ;
;(Ⅱ)若点
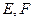 分别在棱上
分别在棱上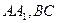 上,且
上,且 ,问点
,问点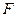 在何处时,
在何处时,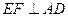 ;
;(Ⅲ)若
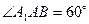 ,求二面角
,求二面角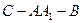 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。
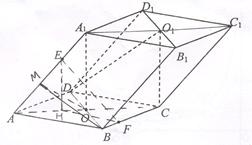
(Ⅰ)连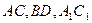 ,则
,则 为
为 的交点,
的交点, 为A
为A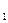 C
C ,
, 的交点。
的交点。
 由平行六面体的性质知:
由平行六面体的性质知: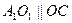 且
且
 四边形
四边形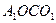 为平行四边形,K]
为平行四边形,K]

又 平面
平面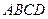
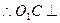 平面
平面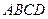
又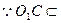 平面
平面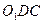
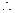 平面
平面 平面
平面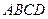
(Ⅱ)作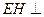 平面
平面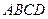 ,垂足为
,垂足为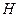 ,
,
则 ,点
,点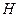 在直线
在直线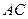 上,
上,
且EF在平面ABCD上的射影 为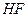 。
。
由三垂线定理及其逆定理,知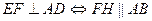
 ,
,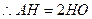 ,从而
,从而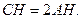 又
又
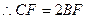
从而
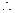 当
当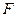 为
为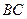 的三等分点(靠近B)时,有
的三等分点(靠近B)时,有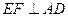
(III)过点 作
作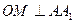 ,垂足为
,垂足为 ,连接
,连接 。
。
 平面ABCD,
平面ABCD,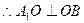
又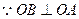
 平面
平面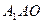 。由三垂线定理得
。由三垂线定理得
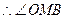 为二面角
为二面角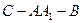 的平面角。
的平面角。
在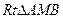 中,
中,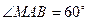 ,
,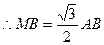
又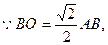
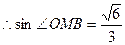
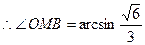
二面角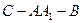 的大小为
的大小为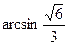
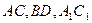 ,则
,则 为
为 的交点,
的交点, 为A
为A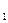 C
C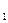 ,
, 的交点。
的交点。 由平行六面体的性质知:
由平行六面体的性质知: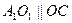 且
且
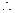 四边形
四边形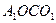 为平行四边形,K]
为平行四边形,K]
又
 平面
平面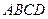
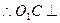 平面
平面
又
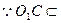 平面
平面
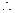 平面
平面 平面
平面
(Ⅱ)作
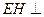 平面
平面 ,垂足为
,垂足为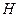 ,
,则
 ,点
,点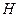 在直线
在直线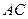 上,
上,且EF在平面ABCD上的射影 为
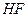 。
。由三垂线定理及其逆定理,知
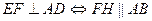
 ,
,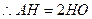 ,从而
,从而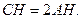 又
又
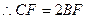
从而

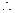 当
当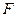 为
为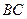 的三等分点(靠近B)时,有
的三等分点(靠近B)时,有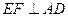
(III)过点
 作
作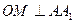 ,垂足为
,垂足为 ,连接
,连接 。
。 平面ABCD,
平面ABCD,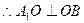
又
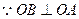
 平面
平面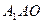 。由三垂线定理得
。由三垂线定理得
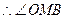 为二面角
为二面角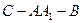 的平面角。
的平面角。在
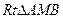 中,
中,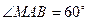 ,
,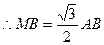
又
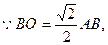
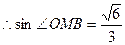
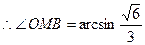
二面角
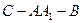 的大小为
的大小为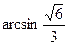
略

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
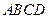 的一组对棱
的一组对棱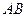 、
、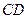 的平面截此四面体(如图).
的平面截此四面体(如图).
 是平行四边形;
是平行四边形;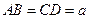 .求证:四边形
.求证:四边形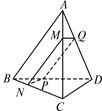
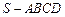 中,
中,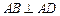 ,
,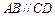 ,
,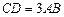 ,平面
,平面 平面
平面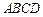 ,
,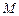 是线段
是线段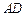 上一点,
上一点,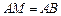 ,
,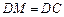 ,
,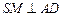 .
.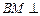 平面
平面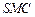 ;
;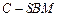 与四棱锥
与四棱锥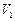 与
与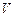 ,求
,求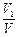 的值.
的值.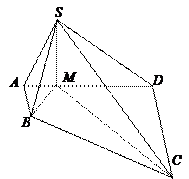
 CD中,
CD中,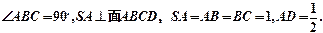

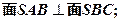
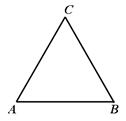
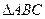 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰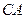 的长为
的长为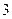 (百米),底
(百米),底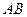 的长为
的长为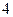 (百米).现决定在空地内筑一条笔直的小路
(百米).现决定在空地内筑一条笔直的小路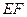 (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为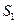 和
和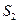 .
.
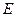 为
为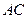 的中点,求此时小路的长度;
的中点,求此时小路的长度;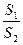 的最小值.
的最小值.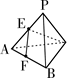
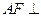 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
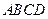 中,
中,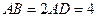 ,
,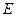 为
为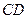 的中点,沿
的中点,沿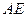 将
将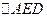 折起,使
折起,使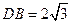 ,
,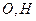 分别为
分别为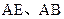 的中点。
的中点。