题目内容
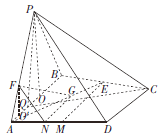
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.

(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,若平面
,若平面![]() 将四棱锥
将四棱锥![]() 分成体积相等的两部分,求三棱锥
分成体积相等的两部分,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)运用线面平行的判定定理推证;(2)借助三棱锥的体积公式求解:
试题解析:
解:(1)![]() 为线段
为线段![]() 的靠近
的靠近![]() 的三等分点.
的三等分点.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
则![]() ,
,
当![]() 为线段
为线段![]() 的靠近
的靠近![]() 的三等分点时,即
的三等分点时,即![]() ,
,![]() .
.
∵![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)∵三棱锥![]() 与四棱锥
与四棱锥![]() 的高相同,
的高相同,
∴![]() 与四边形
与四边形![]() 的面积相等.
的面积相等.
设![]() ,则
,则![]() ,∵
,∵![]() ,
,
∴![]() ,
,
解得![]() .
.
取![]() 中点
中点![]() ,∵
,∵![]() 为正三角形,∴
为正三角形,∴![]() ,∵平面
,∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点的零件的多少随机器的运转的速度的变化而变化,下表为抽样试验的结果:
转速 | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数 | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果![]() 对
对![]() 有线性相关关系,请画出一条直线近似地表示这种线性关系;
有线性相关关系,请画出一条直线近似地表示这种线性关系;
(3)在实际生产中,若它们的近似方程为![]() ,允许每小时生产的产品中有缺点的零件最多为
,允许每小时生产的产品中有缺点的零件最多为![]() 件,那么机器的运转速度应控制在什么范围内?
件,那么机器的运转速度应控制在什么范围内?
