题目内容
4．已知解集A={y|y=2n（n∈N*）}，B={y|y=2n+1，n∈N*}，则A∩B中有（ ）个元素．| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据交集的定义，分别画出y=2x，y=2x+1的图象，即可得到答案．
解答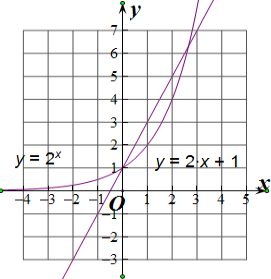 
解：分别画出y=2x，y=2x+1的图象，如图所示，
所以当n=x，n∈N*，没有交点，
故则A∩B中有0个元素．
故选：A
点评 本题考查交集的定义，元素与集合的关系，采用了数形结合的思想，属于基础题．
练习册系列答案
相关题目
14．下列有关命题的说法正确的是（ ）
| A． | 命题“若x2=1，则x=1”的否命题为“若x2≠1，则x≠1” | |
| B． | 命题“若x=y，则sinx=siny”的逆命题为真命题 | |
| C． | 命题“?x0∈R，x${\;}_{0}^{2}$+x0+1=0”的否定是“?x∈R，x2+x+1＜0” | |
| D． | 命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
14．函数$f（x）=sin（\frac{1}{3}x-\frac{π}{3}）$的一个单调增区间为（ ）
| A． | $[-\frac{3}{2}π，π]$ | B． | $[\frac{5}{2}π，3π]$ | C． | $[-\frac{5}{6}π，-\frac{π}{2}]$ | D． | $[-\frac{1}{2}π，\frac{5π}{2}]$ |