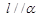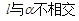题目内容
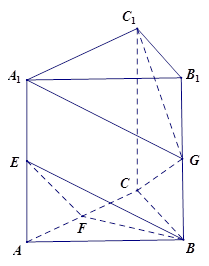
(本题满分14分)如图,在直三棱柱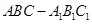 中,
中, ,
,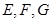 分别是
分别是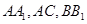 的中点,且
的中点,且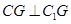 .
.
(1)求证: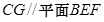 ;
;
(2)求证:平面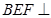 平面
平面 .
.
 中,
中, ,
, 分别是
分别是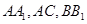 的中点,且
的中点,且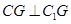 .
. (1)求证:
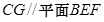 ;
;(2)求证:平面
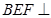 平面
平面 .
.
解:(1)连结AG, 交BE于点M, 连结FM ……………2分
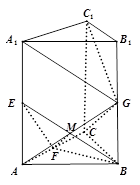
∵E, G分别为棱的中点,
∴四边形ABGE为平行四边形,
∴点M为BE的中点, ……………4分
而点F为AC的中点,∴FM∥CG
∵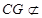 面BEF,
面BEF, 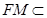 面BEF, ∴
面BEF, ∴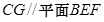 ;………7分
;………7分
(2因为三棱柱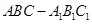 是直三棱柱,,
是直三棱柱,,
∴A1C1⊥面BC1,而CG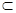 面BC1
面BC1
∴A1C1⊥CG, ….…………….………10分
又∵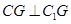 ,∴CG⊥面A1C1G
,∴CG⊥面A1C1G
由(1)知,FM∥CG
∴FM⊥面A1C1G, …………….…………………12分
而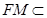 面BEF, ∴平面
面BEF, ∴平面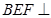 平面
平面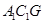 . .…………………14分
. .…………………14分

∵E, G分别为棱的中点,
∴四边形ABGE为平行四边形,
∴点M为BE的中点, ……………4分
而点F为AC的中点,∴FM∥CG
∵
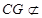 面BEF,
面BEF, 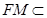 面BEF, ∴
面BEF, ∴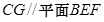 ;………7分
;………7分(2因为三棱柱
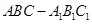 是直三棱柱,,
是直三棱柱,,
∴A1C1⊥面BC1,而CG
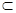 面BC1
面BC1∴A1C1⊥CG, ….…………….………10分
又∵
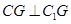 ,∴CG⊥面A1C1G
,∴CG⊥面A1C1G由(1)知,FM∥CG
∴FM⊥面A1C1G, …………….…………………12分
而
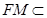 面BEF, ∴平面
面BEF, ∴平面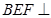 平面
平面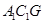 . .…………………14分
. .…………………14分略

练习册系列答案
相关题目
 中,已知点
中,已知点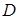 、
、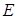 、
、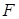 分别为棱
分别为棱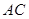 、
、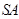 、
、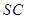 的中点.
的中点. ∥平面
∥平面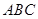 ;
;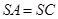 ,
,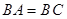 ,求证:平面
,求证:平面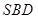 ⊥平面
⊥平面
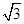 , 点P为矩形ABCD所
, 点P为矩形ABCD所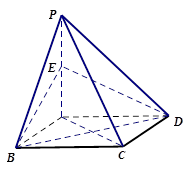
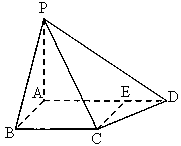
 的各条棱长都为a,P为
的各条棱长都为a,P为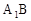 上的点。
上的点。 的值,使得PC⊥AB;
的值,使得PC⊥AB;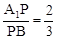 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小; 到平面PAC的距离。
到平面PAC的距离。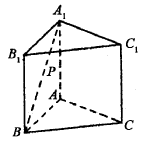
 中,
中,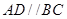 ,
,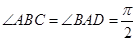 ,
,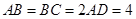 ,
,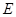 、
、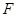 分别是
分别是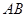 、
、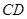 上的动点,且
上的动点,且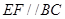 ,设
,设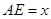 (
(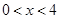 )。沿
)。沿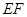 将梯形
将梯形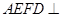 平面
平面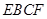 ,如图(2)。
,如图(2)。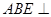 平面
平面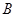 、
、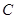 、
、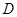 、
、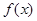 ,求
,求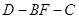 的正弦值.
的正弦值.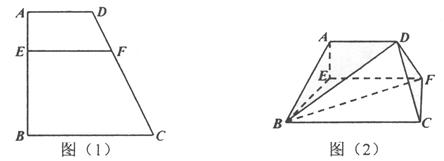
 、
、 .有下列命题
.有下列命题


 平行于平面
平行于平面 内的无数条直线,则下列结论正确的是
内的无数条直线,则下列结论正确的是