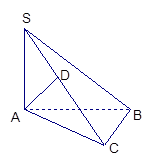
题目内容
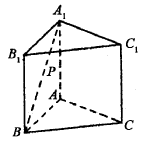
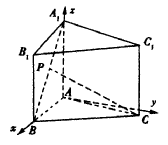
如图,已知正三棱柱 的各条棱长都为a,P为
的各条棱长都为a,P为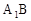 上的点。
上的点。
(1)试确定 的值,使得PC⊥AB;
的值,使得PC⊥AB;
(2)若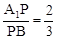 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;
(3)在(2)的条件下,求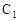 到平面PAC的距离。
到平面PAC的距离。
 的各条棱长都为a,P为
的各条棱长都为a,P为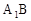 上的点。
上的点。(1)试确定
 的值,使得PC⊥AB;
的值,使得PC⊥AB;(2)若
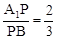 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;(3)在(2)的条件下,求
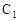 到平面PAC的距离。
到平面PAC的距离。
解:以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA1为z轴,建立空间直角坐标系A—xyz,如图所示,则B(a,0,0),A1(0,0,a),C(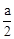 ,
,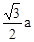 ,0),设P(x,0,z)
,0),设P(x,0,z)
(1)由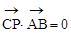 ,得
,得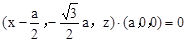
即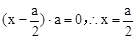 ,∴P为A1B的中点
,∴P为A1B的中点
即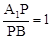 时,PC⊥AB . ……………………3分
时,PC⊥AB . ……………………3分
(2)当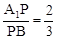 时,由
时,由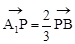 ,得(x,0,z-a)
,得(x,0,z-a)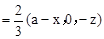
即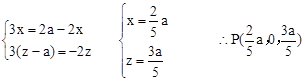
设平面PAC的一个法向量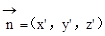
则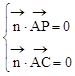 ,即
,即
即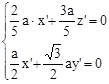
取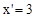 ,则
,则
∴
又平面ABC的一个法向量为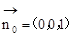
∴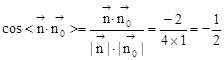
∴二面角P—AC—B的大小为180°-120°=60°………………7分
(3)设C1到平面PAC的距离为d
则
即C1到平面PAC的距离为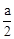 . ……………………10分
. ……………………10分
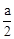 ,
,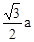 ,0),设P(x,0,z)
,0),设P(x,0,z)
(1)由
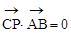 ,得
,得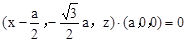
即
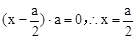 ,∴P为A1B的中点
,∴P为A1B的中点即
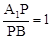 时,PC⊥AB . ……………………3分
时,PC⊥AB . ……………………3分(2)当
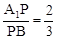 时,由
时,由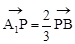 ,得(x,0,z-a)
,得(x,0,z-a)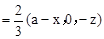
即
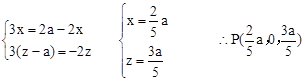
设平面PAC的一个法向量
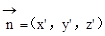
则
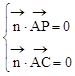 ,即
,即
即
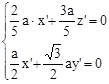
取
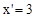 ,则
,则
∴

又平面ABC的一个法向量为
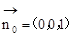
∴
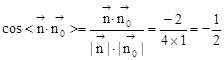
∴二面角P—AC—B的大小为180°-120°=60°………………7分
(3)设C1到平面PAC的距离为d
则

即C1到平面PAC的距离为
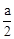 . ……………………10分
. ……………………10分略

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
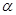 ,
,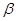 ,直线a,b,给出以下命题,正确的是( )
,直线a,b,给出以下命题,正确的是( )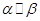
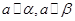 ,且a不在
,且a不在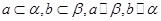 ,则
,则 ,有以下几个命题,其中是真命题的序号为 。(1)若
,有以下几个命题,其中是真命题的序号为 。(1)若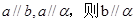 (2)
(2)
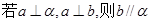 (4)
(4)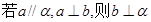
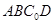 中,
中,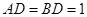 ,
,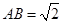 。沿它的对角线
。沿它的对角线 把△
把△ 折起,使点
折起,使点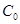 到达平面
到达平面 的位置。
的位置。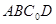 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角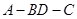 的大小。
的大小。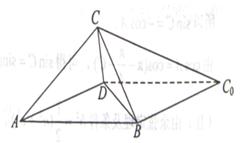
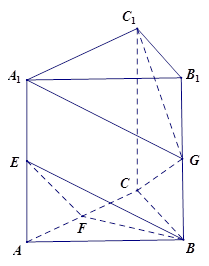
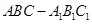 中,
中, ,
,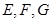 分别是
分别是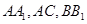 的中点,且
的中点,且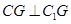 .
. 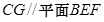 ;
;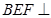 平面
平面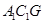 .
.
 ,
, ,直线
,直线 ,若
,若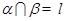 ,则
,则  所在的平面垂直于矩形
所在的平面垂直于矩形 所在的平面,
所在的平面,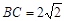 ,
,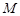 为
为 的中点.
的中点.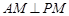 ;
;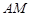 和
和 所成角的余弦值.
所成角的余弦值.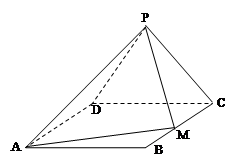
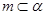 且
且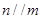 ,则
,则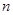 与
与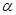 的位置关系是 ( )
的位置关系是 ( )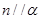
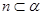
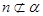
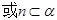
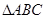 中
中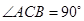 ,
,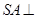 面
面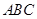 ,
,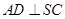 ,求证:
,求证: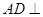 面
面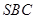 .
.