Question

【题目】如图，直三棱柱ABC﹣A1B1C1的底面为直角三角形，两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．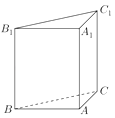
（1）求三棱柱ABC﹣A1B1C1的体积；
（2）设M是BC中点，求直线A1M与平面ABC所成角的大小．

Answer 1

【答案】
（1）解：∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，

两直角边AB和AC的长分别为4和2，侧棱AA1的长为5．

∴三棱柱ABC﹣A1B1C1的体积：

V=S△ABC×AA1

=

= =20

（2）解：连结AM，

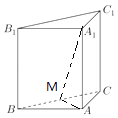
∵直三棱柱ABC﹣A1B1C1的底面为直角三角形，

两直角边AB和AC的长分别为4和2，侧棱AA1的长为5，M是BC中点，

∴AA1⊥底面ABC，AM= = ，

∴∠A1MA是直线A1M与平面ABC所成角，

tan∠A1MA= = = ，

∴直线A1M与平面ABC所成角的大小为arctan ．

【解析】（1）三棱柱ABC﹣A1B1C1的体积V=S△ABC×AA1= ，由此能求出结果．（2）连结AM，∠A1MA是直线A1M与平面ABC所成角，由此能求出直线A1M与平面ABC所成角的大小．