题目内容
已知函数 的定义域为R,当
的定义域为R,当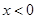 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且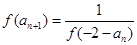 (
( ),则
),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
B
解析试题分析:在 中令
中令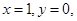 则式子变为
则式子变为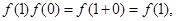 因为当
因为当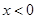 时,
时, ,
,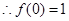 ,即
,即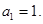 由
由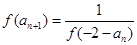 可得
可得 ,即
,即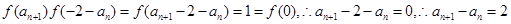 ,所以数列
,所以数列 是以1为首项,以2为公差的等差数列,所以
是以1为首项,以2为公差的等差数列,所以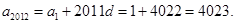
考点:本小题主要考查抽象函数,等差数列.
点评:解决抽象函数问题,常用的方法是“赋值法”,而解决本题的关键是通过赋值,将抽象函数问题转化为等差数列问题.

练习册系列答案
相关题目
三个数 ,
,  ,
,  的大小顺序为 ( )
的大小顺序为 ( )
A. | B. |
C.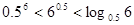 | D. |
函数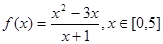 的值域是( )
的值域是( )
| A.[0,2] | B.[0,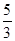 ] ] | C.[-1,2] | D.[-1,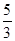 ] ] |
函数 的零点所在的区间是
的零点所在的区间是
A. | B. | C. | D.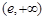 |
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C.1 | D.3 |
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 ,则
,则 可以是
可以是
A. | B. |
C. | D. |



 与
与 (
( 且
且 )的图象可能是( )
)的图象可能是( )



