题目内容
15．
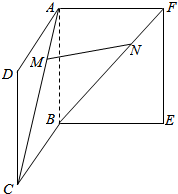如图所示，已知正方形ABCD和ABEF，M、N是AC、BF上的点且AM=FN，求证：MN∥面BCE．
分析 作MG∥AB交BC于G，作NH∥EF交BE于H．连结GH，先运用线段比例关系证明出MG=NH，且MG∥NH．推断出MNGH为平行四边形，进而证明出MN∥GH，最后利用线面平行的判定定理证明出结论．
解答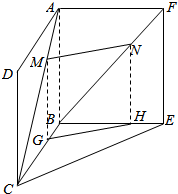 
解：作MG∥AB交BC于G，作NH∥EF交BE于H．
连结GH，
则CM：CA=MG：AB，BN：BF=NH：EF，
又AM=FN，AC=BF，故CM=BN，
∴MG=NH，且MG∥NH．
∴MNGH为平行四边形，
∴MN∥GH．
GH?平面BCE，MN?平面BCE，
∴MN∥平面BCE．
点评 本题主要考查了线面平行的判定定理的运用．解题的关键是证明出MN∥GH，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
20．把直线x-y+1=0沿向量$\overrightarrow{a}$=（1，0）方向平移，使之与圆（x-2）2+（y-1）2=1相切，则平移的距离为（ ）
| A． | $\sqrt{2}-1$ | B． | $\sqrt{2}+2$ | C． | $\sqrt{2}-1$与$\sqrt{2}+1$ | D． | 2-$\sqrt{2}$与2+$\sqrt{2}$ |