题目内容
8.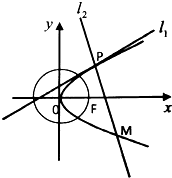 如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4
如图,已知圆O:x2+y2=a2(a>0)过抛物线C:y2=2px(p>0)的焦点F,过点F且与圆O相切的直线被抛物线C截得的弦长为4(1)求圆O和抛物线C的标准方程;
(2)若P为抛物线C在第一象限内的点,抛物线在点P处的切线y=kx+b(设为l1)被圆O截得的弦长为$\frac{\sqrt{95}}{5}$,直线l2过点P且垂直直线l1,设l2与抛物线的另一交点为M,求弦PM的长.
分析 (1)通过抛物线C的方程可得焦点F($\frac{p}{2}$,0),利用圆O:x2+y2=a2(a>0)过点F可知a=$\frac{p}{2}$,利用过点F且与圆O相切的直线被抛物线C截得的弦长为4可得p=2,进而可得a=1,从而可得结论;
(2)通过直线l1与抛物线方程,利用△=0可得kb=1,利用点O到直线的距离d=$\frac{|b|}{\sqrt{1+{k}^{2}}}$与l1被圆O截得的弦长为2$\sqrt{1-{d}^{2}}$=$\frac{\sqrt{95}}{5}$,计算可得k=2、b=$\frac{1}{2}$,代入ky2-4y+4b=0得y=1,将y=1代入抛物线方程y2=4x得P($\frac{1}{4}$,1),联立l2与抛物线的方程可得M($\frac{81}{4}$,-9),进而可得结论.
解答 解:(1)由抛物线C:y2=2px(p>0)的方程可得焦点F($\frac{p}{2}$,0),
又圆O:x2+y2=a2(a>0)过点F,∴a=$\frac{p}{2}$,
又∵过点F且与圆O相切的直线被抛物线C截得的弦长为4,
∴2p=4,∴p=2,a=1,
∴圆O的标准方程为:x2+y2=1,
抛物线C的标准方程为:y2=4x;
(2)依题意可知直线l1的斜率k>0,
联立$\left\{\begin{array}{l}{y=kx+b}\\{{y}^{2}=4x}\end{array}\right.$,消去x整理得:ky2-4y+4b=0,
由△=16-16kb=0,可得kb=1,
∵点O到直线的距离d=$\frac{|b|}{\sqrt{1+{k}^{2}}}$,
∴l1被圆O截得的弦长为2$\sqrt{1-{d}^{2}}$=2$\sqrt{1-\frac{{b}^{2}}{1+{k}^{2}}}$=2$\sqrt{1-\frac{1}{{k}^{2}(1+{k}^{2})}}$=$\frac{\sqrt{95}}{5}$,
化简得:k4+k2-20=0,解得k=2(k=-2舍去),
又kb=1,∴b=$\frac{1}{2}$,
将k=2、b=$\frac{1}{2}$代入ky2-4y+4b=0,得y=1,
将y=1代入抛物线方程y2=4x,得P($\frac{1}{4}$,1),
∴l2的斜率为-$\frac{1}{2}$,故l2的方程为:y-1=-$\frac{1}{2}$(x-$\frac{1}{4}$),即y=-$\frac{1}{2}$x+$\frac{9}{8}$,
联立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{9}{8}}\\{{y}^{2}=4x}\end{array}\right.$,消去x整理得:y2+8y-9=0,
由韦达定理可知:yPyM=9,
又∵P($\frac{1}{4}$,1)∴yM=-9,进而可得M($\frac{81}{4}$,-9),
∴|PM|=$\sqrt{(\frac{81}{4}-\frac{1}{4})^{2}+(-9-1)^{2}}$=10$\sqrt{5}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.
如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB,$PA=2\sqrt{10}$,PB=4,则线段AB的长为2$\sqrt{3}$.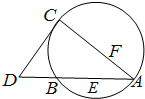 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.