题目内容
判断下列函数的奇偶性:
(1)f(x)=x4+x;
(2)f(x)=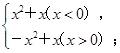
(3)f(x)=lg(x+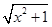 ).
).
(1)f(x)=x4+x;
(2)f(x)=
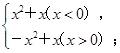
(3)f(x)=lg(x+
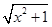 ).
).(1)既不是奇函数也不是偶函数(2)奇函数(3)奇函数
(1)定义域为R,f(-1)=0,f(1)=2,由于f(-1)≠f(1),f(-1)≠-f(1),所以f(x)既不是奇函数也不是偶函数;
(2)因为函数f(x)的定义域是(-∞,0)∪(0,+∞),并且当x<0时,-x>0,所以f(-x)=-(-x)2+(-x)=-(x2+x)=-f(x)(x<0).当x>0时,-x<0,所以f(-x)=(-x)2+(-x)=-(-x2+x)=-f(x)(x>0).故函数f(x)为奇函数.
(3)由x+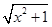 >0,得x∈R,由f(-x)+f(x)=lg(-x+
>0,得x∈R,由f(-x)+f(x)=lg(-x+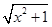 )+lg(x+
)+lg(x+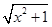 )=lg1=0,所以f(-x)=-f(x),所以f(x)为奇函数.
)=lg1=0,所以f(-x)=-f(x),所以f(x)为奇函数.
(2)因为函数f(x)的定义域是(-∞,0)∪(0,+∞),并且当x<0时,-x>0,所以f(-x)=-(-x)2+(-x)=-(x2+x)=-f(x)(x<0).当x>0时,-x<0,所以f(-x)=(-x)2+(-x)=-(-x2+x)=-f(x)(x>0).故函数f(x)为奇函数.
(3)由x+
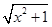 >0,得x∈R,由f(-x)+f(x)=lg(-x+
>0,得x∈R,由f(-x)+f(x)=lg(-x+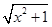 )+lg(x+
)+lg(x+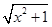 )=lg1=0,所以f(-x)=-f(x),所以f(x)为奇函数.
)=lg1=0,所以f(-x)=-f(x),所以f(x)为奇函数.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
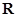 上的函数
上的函数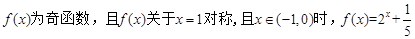 ,则
,则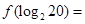 ___ ______ 。
___ ______ 。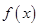 是定义在
是定义在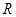 上的奇函数,若它的最小正周期为
上的奇函数,若它的最小正周期为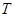 ,则
,则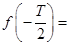 ________
________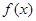 是定义在
是定义在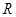 上的偶函数,
上的偶函数,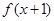 为奇函数,
为奇函数,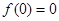 ,当
,当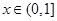 时,
时,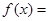 log2x,则在
log2x,则在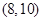 内满足方程
内满足方程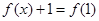 的实数
的实数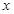 为
为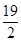
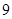
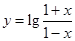
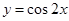
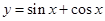
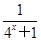 是奇函数,则常数a=________.
是奇函数,则常数a=________.