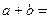题目内容
已知数列{an}有a1 = a,a2 = p(常数p > 0),对任意的正整数n,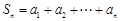 ,且
,且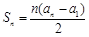 .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式;若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b,使得对任意的正整数n都有bn< b,且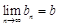 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令 ,求数列
,求数列 的“上渐近值”.
的“上渐近值”.
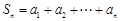 ,且
,且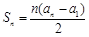 .
.(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式;若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b,使得对任意的正整数n都有bn< b,且
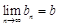 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令 ,求数列
,求数列 的“上渐近值”.
的“上渐近值”.(1)a = 0
(2)an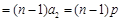
(3)数列 的“上渐近值”为3
的“上渐近值”为3
(2)an
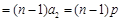
(3)数列
 的“上渐近值”为3
的“上渐近值”为3(1) 由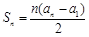 知
知
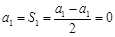 ∴ a =" 0 " ················ 3分
∴ a =" 0 " ················ 3分
(2) 由 (1)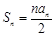 ,
,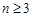 时,
时,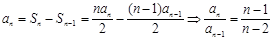 4分
4分
∴
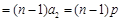 ····················· 6分
····················· 6分
显然an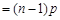 对a1,a2适合
对a1,a2适合
∴ 数列{an}是以0为首项,p为公差的等差数列··········· 7分
(3) 由(2)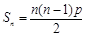 ,
,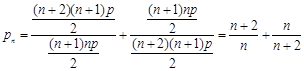 8分
8分
∴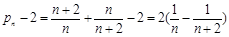 ·············· 10分
·············· 10分
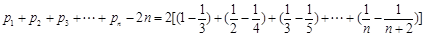
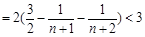 ····················· 11分
····················· 11分
∴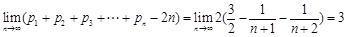 ····· 12分
····· 12分
∴数列 的“上渐近值”为3·········· 13分
的“上渐近值”为3·········· 13分
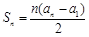 知
知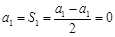 ∴ a =" 0 " ················ 3分
∴ a =" 0 " ················ 3分(2) 由 (1)
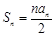 ,
,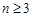 时,
时,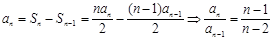 4分
4分∴

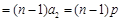 ····················· 6分
····················· 6分显然an
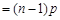 对a1,a2适合
对a1,a2适合∴ 数列{an}是以0为首项,p为公差的等差数列··········· 7分
(3) 由(2)
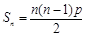 ,
,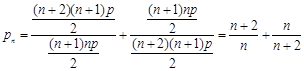 8分
8分∴
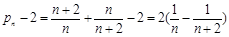 ·············· 10分
·············· 10分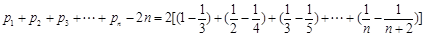
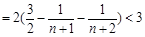 ····················· 11分
····················· 11分∴
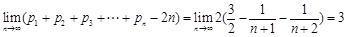 ····· 12分
····· 12分∴数列
 的“上渐近值”为3·········· 13分
的“上渐近值”为3·········· 13分
练习册系列答案
相关题目
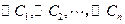 是圆心在抛物线
是圆心在抛物线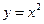 上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为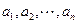 ,已知
,已知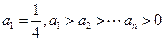 ,又
,又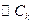
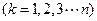 都与
都与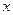 轴相切,且顺次逐个相邻外切.
轴相切,且顺次逐个相邻外切. 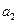 ;
;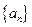 的通项公式;
的通项公式;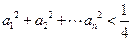 .
.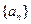 中,
中,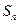 为
为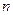 项和,
项和,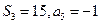 .
.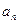 与
与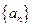 满足:
满足: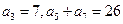 .
.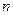 项和为
项和为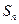 。
。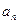 及
及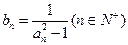 ,求数列
,求数列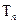 .
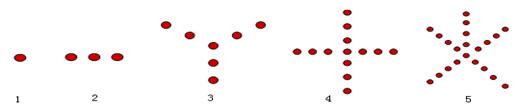
.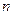 个图形中的点数
个图形中的点数 .
.
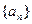 中,
中,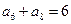 ,则数列
,则数列
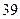
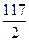
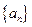 是等差数列,
是等差数列,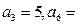 11且,
11且,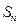 是数列
是数列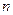 项和。
项和。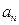 及前
及前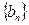 满足
满足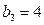 ,
,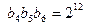 ,数列
,数列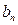
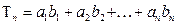 ,求
,求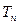 的值。
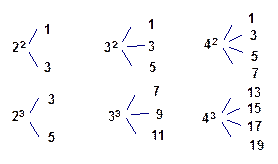
的值。 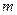 的
的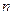 次幂可用奇数进行如图所示的“分裂”,仿此,记
次幂可用奇数进行如图所示的“分裂”,仿此,记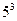 的“分裂”中的最小数为
的“分裂”中的最小数为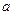 ,而
,而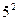 的“分裂”中最大的数是
的“分裂”中最大的数是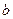 ,则
,则