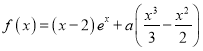ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥÷–―ß”–ΫΧ Π400»ΥΘ§Τδ÷–ΗΏ÷–ΫΧ Π240»Υ.ΈΣΝΥΝΥΫβΗΟ–ΘΫΧ ΠΟΩΧλΩΈΆβΕΆΝΕ ±ΦδΘ§œ÷άϊ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”ΗΟ–ΘΫΧ Π÷–ΥφΜζ≥ι»ΓΝΥ100ΟϊΫΧ ΠΫχ––Βς≤ιΘ§Ά≥ΦΤΤδΟΩΧλΩΈΆβΕΆΝΕ ±Φδ(Υυ”–ΫΧ ΠΟΩΧλΩΈΆβΕΆΝΕ ±ΦδΨυ‘Ύ![]() Ζ÷÷”ΡΎ)Θ§ΫΪΆ≥ΦΤ ΐΨίΑ¥
Ζ÷÷”ΡΎ)Θ§ΫΪΆ≥ΦΤ ΐΨίΑ¥![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Γ≠Θ§
Θ§Γ≠Θ§![]() Ζ÷≥…6ΉιΘ§÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ
Ζ÷≥…6ΉιΘ§÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ
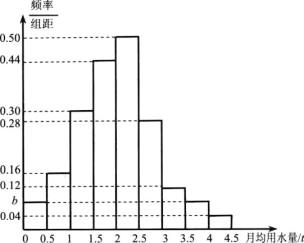
ΦΌ…ηΟΩΈΜΫΧ ΠΟΩΧλΩΈΆβΕΆΝΕ ±ΦδœύΜΞΕάΝΔΘ§≤Δ≥ΤΟΩΧλΕΆΝΕ ±Φδ–Γ”Ύ20Ζ÷÷”ΈΣ»±ΖΠΕΆΝΕ.
Θ®1Θ© ‘ΙάΦΤ±Ψ–ΘΫΧ Π÷–»±ΖΠΕΆΝΕΒΡ»Υ ΐΘΜ
Θ®2Θ©»τ¥”≤Έ”κΒς≤ιΘ§«“ΟΩΧλΩΈΆβΕΆΝΕ ±Φδ‘Ύ![]() ΡΎΒΡΗΟ–ΘΫΧ Π÷–»Έ»Γ2»ΥΘ§«σ÷Ν…Ό”–1Οϊ≥θ÷–ΫΧ Π±Μ―Γ÷–ΒΡΗ≈¬ .
ΡΎΒΡΗΟ–ΘΫΧ Π÷–»Έ»Γ2»ΥΘ§«σ÷Ν…Ό”–1Οϊ≥θ÷–ΫΧ Π±Μ―Γ÷–ΒΡΗ≈¬ .
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() »Υ.Θ®2Θ©
»Υ.Θ®2Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σΒΟ―υ±Ψ÷–≥θ÷–ΓΔΗΏ÷–ΫΧ Π»±ΖΠΕΆΝΕΒΡΤΒ¬ Θ§”…¥ΥΦΤΥψ≥ωΗΟ–ΘΫΧ Π÷–»±ΖΠΕΆΝΕΒΡ»Υ ΐ.άϊ”ΟΝ–ΨΌΖ®Θ§ΫαΚœΙ≈ΒδΗ≈–ΆΗ≈¬ ΦΤΥψΙΪ ΫΘ§ΦΤΥψ≥ωΥυ«σΗ≈¬ .
Θ®2Θ©άϊ”ΟΝ–ΨΌΖ®Θ§ΫαΚœΙ≈ΒδΗ≈–ΆΗ≈¬ ΦΤΥψΙΪ ΫΘ§ΦΤΥψ≥ωΥυ«σΗ≈¬ .
Θ®1Θ©”…Χβ“βΩ…ΒΟ―υ±Ψ÷–≥θ÷–ΫΧ Π»±ΖΠΕΆΝΕΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
―υ±Ψ÷–ΗΏ÷–ΫΧ Π»±ΖΠΕΆΝΕΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
ΙάΦΤΗΟ–ΘΫΧ Π÷–»±ΖΠΕΆΝΕΒΡ»Υ ΐΈΣ![]() .
.
Θ®2Θ©”…Χβ“βΩ…≤Έ”κΒς≤ι≥θ÷–ΫΧ ΠΟΩΧλΩΈΆβΕΆΝΕ ±Φδ‘Ύ![]() ΒΡ»Υ ΐΈΣ
ΒΡ»Υ ΐΈΣ![]() Θ§Φ«ΈΣ
Θ§Φ«ΈΣ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
ΗΏ÷–ΫΧ ΠΟΩΧλΩΈΆβΕΆΝΕ ±Φδ‘Ύ![]() ΒΡ»Υ ΐΈΣ
ΒΡ»Υ ΐΈΣ![]() Θ§Φ«ΈΣ
Θ§Φ«ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
¥”’β5»Υ÷–―Γ»Γ2»ΥΒΡ«ιΩω”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Ι≤10÷÷ΘΜ
Θ§Ι≤10÷÷ΘΜ
Τδ÷–ΖϊΚœΧθΦΰΒΡ«ιΩω”–![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§Ι≤7÷÷.
Θ§Ι≤7÷÷.
Ι Υυ«σΗ≈¬ ![]() .
.

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥ΙΪΥΨA≤ζΤΖ…ζ≤ζΒΡΆΕ»κ≥…±ΨxΘ®ΒΞΈΜΘΚΆρ‘ΣΘ©”κ≤ζΤΖœζ έ ’»κyΘ®ΒΞΈΜΘΚ °Άρ‘ΣΘ©¥φ‘ΎΫœΚΟΒΡœΏ–‘ΙΊœΒΘ§œ¬±μΦ«¬ΦΝΥΗΟΙΪΥΨΉνΫϋ8¥ΈΗΟ≤ζΤΖΒΡœύΙΊ ΐΨίΘ§«“ΗυΨί’β8Ήι ΐΨίΦΤΥψΒΟΒΫyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() Θ°
Θ°
xΘ®Άρ‘ΣΘ© | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
yΘ® °Άρ‘ΣΘ© | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
Θ®1Θ©«σ![]() ΒΡ÷ΒΘ®ΫαΙϊΨΪ»ΖΒΫ0.0001Θ©Θ§≤ΔΙάΦΤΙΪΥΨA≤ζΤΖΆΕ»κ≥…±Ψ30Άρ‘ΣΚσ≤ζΤΖΒΡœζ έ ’»κΘ®ΒΞΈΜΘΚ °Άρ‘ΣΘ©Θ°
ΒΡ÷ΒΘ®ΫαΙϊΨΪ»ΖΒΫ0.0001Θ©Θ§≤ΔΙάΦΤΙΪΥΨA≤ζΤΖΆΕ»κ≥…±Ψ30Άρ‘ΣΚσ≤ζΤΖΒΡœζ έ ’»κΘ®ΒΞΈΜΘΚ °Άρ‘ΣΘ©Θ°
Θ®2Θ©ΗΟΙΪΥΨB≤ζΤΖ…ζ≤ζΒΡΆΕ»κ≥…±ΨuΘ®ΒΞΈΜΘΚΆρ‘ΣΘ©”κ≤ζΤΖœζ έ ’»κvΘ®ΒΞΈΜΘΚ °Άρ‘ΣΘ©“≤¥φ‘ΎΫœΚΟΒΡœΏ–‘ΙΊœΒΘ§«“vΙΊ”ΎuΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() Θ°
Θ°
Θ®iΘ©ΙάΦΤΗΟΙΪΥΨB≤ζΤΖΆΕ»κ≥…±Ψ30Άρ‘ΣΚσΒΡΟΪάϊ¬ Θ®ΟΪάϊ¬ ![]() Θ©ΘΜ
Θ©ΘΜ
Θ®iiΘ©≈–ΕœΗΟΙΪΥΨAΘ§BΝΫΗω≤ζΤΖΕΦΆΕ»κ≥…±Ψ30Άρ‘ΣΚσΘ§ΡΡΗω≤ζΤΖΒΡΟΪάϊ¬ Ηϋ¥σΘ°
ΓΨΧβΡΩΓΩΈ“Ιζ–¬–ΆΙΎΉ¥≤ΓΕΨΖΈ―Ή“Ώ«ιΤΎΦδΘ§“‘Άχ¬γΙΚΈοΚΆΆχ…œΖΰΈώΥυ¥ζ±μΒΡ–¬–ΥœϊΖ―’Ιœ÷≥ωΝΥ«Ω¥σΒΡ…ζΟϋΝΠΘ§–¬–ΥœϊΖ―ΫΪ≥…ΈΣΈ“ΙζœϊΖ―‘ω≥ΛΒΡ–¬Ε·Ρή.Ρ≥ –ΈΣΝΥΝΥΫβ±ΨΒΊΨ”Οώ‘Ύ2020Ρξ2‘¬÷Ν3‘¬ΝΫΗω‘¬Άχ¬γΙΚΈοœϊΖ―«ιΩωΘ§‘ΎΆχ…œΥφΜζΕ‘1000»ΥΉωΝΥΈ ΨμΒς≤ιΘ§ΒΟ»γœ¬ΤΒ ΐΖ÷≤Φ±μΘΚ
ΆχΙΚœϊΖ―«ιΩωΘ®‘ΣΘ© |
|
|
|
|
|
ΤΒ ΐ | 300 | 400 | 180 | 60 | 60 |
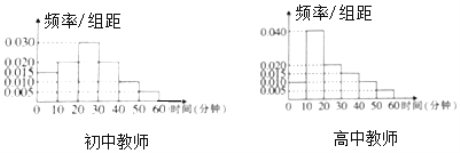
Θ®1Θ©Ής≥ω’β–© ΐΨίΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§≤ΔΙάΦΤ±Ψ –Ψ”Οώ¥ΥΤΎΦδΆχ¬γΙΚΈοΒΡœϊΖ―ΤΫΨυ÷ΒΘΜ
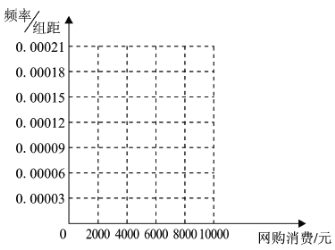
Θ®2Θ©‘ΎΒς≤ιΈ Ψμ÷–”–“Μœν «Χν–¥±Ψ»ΥΡξΝδΘ§ΈΣ―–ΨΩΆχΙΚΫπΕνΚΆΆχΙΚ»ΥΡξΝδΒΡΙΊœΒΘ§“‘ΆχΙΚΫπΕν «Ζώ≥§Ιΐ4000‘ΣΈΣ±ξΉΦΫχ––Ζ÷≤ψ≥ι―υΘ§¥”…œ ω1000»Υ÷–≥ι»Γ200»ΥΘ§ΒΟΒΫ»γœ¬Ν–ΝΣ±μΘ§«κΫΪ±μ≤Ι≥δΆξ’ϊ≤ΔΗυΨίΝ–ΝΣ±μ≈–ΕœΘ§‘Ύ¥ΥΤΎΦδ «Ζώ”–95%ΒΡΑ―Έ’»œΈΣΆχΙΚΫπΕν”κΆχΙΚ»ΥΡξΝδ”–ΙΊ.
ΆχΙΚ≤Μ≥§Ιΐ4000‘Σ | ΆχΙΚ≥§Ιΐ4000‘Σ | ΉήΦΤ | |
40Υξ“‘…œ | 75 | 100 | |
40Υξ“‘œ¬Θ®Κ§40ΥξΘ© | |||
ΉήΦΤ | 200 |
≤ΈΩΦΙΪ ΫΚΆ ΐΨίΘΚ![]() .Θ®Τδ÷–
.Θ®Τδ÷–![]() ΈΣ―υ±Ψ»ίΝΩΘ©
ΈΣ―υ±Ψ»ίΝΩΘ©
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |