Question

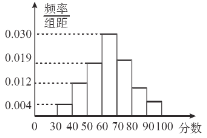
【题目】我国是世界上严重缺水的归家之一，某市为了制订合理的节水方案，对家庭用水情况进行了抽样调查，获得了某年100个家庭的月均用水量（单位：）的数据，将这些数据按照，，，，，，，，分成9组，制成了如图所示的频率分布直方图.

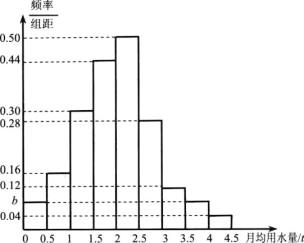
（1）求图中的值，若该市有30万个家庭，试估计全市月均用水量不低于的家庭数；

（2）假设同组中的每个数据都用该组区间的中点值代替，试估计全市家庭月均用水量的平均数；

（3）现从月均用水量在，的家庭中，先按照分层抽样的方法抽取9个家庭，再从这9家庭中抽取4个家庭，记这4个家庭中月均用水量在中的数量为，求的分布列及数学期望.

Answer 1

【答案】（1），36000；（2）2.02；（3）分布列见解析，

【解析】

（1）由题意，解得，由此可得全市月均用水量不低于的家庭所占比例为12%，从而求出答案；

（2）直接根据平均数的计算公式求解即可；

（3）按照分层抽样抽取9个家庭，即抽3家，抽6家，因此可能的取值为1,2,3,4，根据概率计算公式即可求出的分布列，再根据期望的计算公式即可求出期望．

解：（1）∵频率分布直方图中所有矩形的面积之和为1，

∴，解得，

∴月均用水量不低于的家庭所占比例，

因此估计全市月均用水量不低于的家庭所占比例为12%，

家庭数约为；

（2）因为，

因此估计全市家庭月均用水量的平均数为2.02；

（3）在月均用水量，中，有4家，有8家，共12家，

按照分层抽样抽取9个家庭，即抽3家，抽6家，

因此可能的取值为1,2,3,4，

其中，，

，，

∴的分布列如下表所示：

	1	2	3	4

数学期望．