题目内容
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)记F(x)=f(x)﹣g(x),判断F(x)在区间(1,2)内零点个数并说明理由;
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并给出对应的证明.
【答案】解:由题意:F(x)=f(x)﹣g(x),那么:F(x)=xlnx﹣ ![]() .定义域为(0,+∞)
.定义域为(0,+∞)
F′(x)=1+lnx+ ![]() ,由题设x∈(1,2),故F′(x)>0,即F(x)在区间(1,2)上是增函数.(1,2)是单调增区间.那么:F(1)=ln1﹣
,由题设x∈(1,2),故F′(x)>0,即F(x)在区间(1,2)上是增函数.(1,2)是单调增区间.那么:F(1)=ln1﹣ ![]() =
= ![]() <0,F(2)=2ln2﹣
<0,F(2)=2ln2﹣ ![]() >0,并且F(x)在(1,2)上连续的,故根据零点定理,有F(x)在区间(1,2)有且仅有唯一实根,即一个零点.
>0,并且F(x)在(1,2)上连续的,故根据零点定理,有F(x)在区间(1,2)有且仅有唯一实根,即一个零点.
(Ⅱ)记(Ⅰ)中的F(x)在(1,2)内的零点为x0 , 由f(x)=xlnx,当0<x≤1时,f(x)≤0,而g(x)= ![]() >0,故f(x)<g(x);
>0,故f(x)<g(x);
由(Ⅰ)可知F′(x)=1+lnx+ ![]() ,当x>1时,F′(x)>0,存在零点x0∈(1,2),不然有:F(x0)=f(x0)﹣g(x0)=0,故1<x<x0时,f(x)<g(x);当x>x0时,f(x)>g(x);
,当x>1时,F′(x)>0,存在零点x0∈(1,2),不然有:F(x0)=f(x0)﹣g(x0)=0,故1<x<x0时,f(x)<g(x);当x>x0时,f(x)>g(x);
而此得到m(x)= 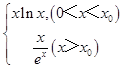 ,
,
显然:当1<x<x0时,m′(x)=1+lnx恒大于0,m(x)是单增函数.
当x>x0时,m′(x)= ![]() 恒小于0,m(x)是单减函数.
恒小于0,m(x)是单减函数.
m(x)=n(n∈R)在(1,+∞)有两个不等实根x1 , x2(x1<x2),则x1∈(1,x0),x2∈(x0 , +∞),
显然:当x2→+∞时,x1+x2>2x0 .
要证明x1+x2>2x0 , 即可证明x2>2x0﹣x1>x0 , 而m(x)在x>x0时是单减函数.故证m(x2)<m(2x0﹣x1).
又由m(x1)=m(x2),即可证:m(x1)<m(2x0﹣x1).即x1lnx1< ![]() ,(构造思想)
,(构造思想)
令h(x)=xlnx﹣ ![]() ,由(1<x<x0).其中h(x0)=0,
,由(1<x<x0).其中h(x0)=0,
那么:h′(x)=1+lnx+ ![]() ﹣
﹣ ![]() ,
,
记φ(t)= ![]() ,则φ′(t)=
,则φ′(t)= ![]() ,当t∈(0,1)时,φ′(t)>0;当t>1时,φ′(t)<0;故φ(t)max=
,当t∈(0,1)时,φ′(t)>0;当t>1时,φ′(t)<0;故φ(t)max= ![]() ;
;
而φ(t)>0;故 ![]() >φ(t)>0,而2x0﹣x>0,从而有:
>φ(t)>0,而2x0﹣x>0,从而有: ![]() <0;
<0;
因此:h′(x)=1+lnx+ ![]() ﹣
﹣ ![]() >0,即h(x)单增,从而1<x<x0时,h(x)<h(x0)=0.
>0,即h(x)单增,从而1<x<x0时,h(x)<h(x0)=0.
即x1lnx1< ![]() 成立.
成立.
故得:x1+x2>2x0 .
【解析】(Ⅰ)对F(x)求导,利用x∈(1,2)判定导函数的符号,进而得到函数的单调性,在利用零点存在定理进行证明.(Ⅱ)先由x的范围讨论f(x),g(x)的大小,确定之间的关系式m(x),在判断x1+x2与2x0的大小,可以利用分析法对其进行证明.
【考点精析】本题主要考查了函数的极值与导数和函数的零点与方程根的关系的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.
是极小值;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.